
Java for-Schleife
Ideen: A. M. Maier, G. Kompa, Elektronikschule Tettnang
E. Fuchst, "Java 9 Grundlagen Programmierung, Herdt Verlag, 2017
In Java wird in der for-Schleife eine feste Anzahl an Wiederholungen durchlaufen. Dazu verwendet man eine Zählvariable.
In diesem Artikel lernst Du die Struktur der for-Schleife in Java kennen. Neben der Schleifenstruktur mit Initialisierung, Bedingung und Änderung, wird das Inkrementieren, Dekrementieren und die verschachtelte for-Schleife erklärt.
Ice Age und der Ländercode Die Struktur der for-Schleife
Als meine Frau aus China die DVD ICE Age für 1 EUR mitbrachte war die Freude unserer Kids groß. Umso überraschter war ich, als beim DVD-Player die Ländercodemeldung kam:
Aktuelle Region: Europa
Mögliche Änderungen: 7
Zähler zum Einstellen der Region: 0mal geändert
Das musste ich natürlich gleich ausprobieren. Ich wechselte auf die Region China und dann wieder zurück auf Europa und schon hatte ich nur noch 5 mögliche Änderungen. Das zusätzlichen funktionierte. Nach jedem Wechsel war ich um eine Änderungsmöglichkeit ärmer.
Nach einem ganz ähnlichen Prinzip funktioniert auch die for-Schleife oder Zählschleife in Java.
Die for-Schleife in Java Syntax
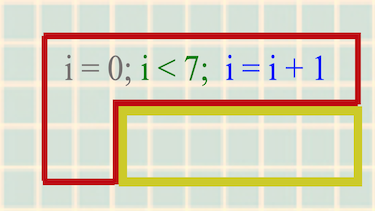
In Java wird in der for-Schleife (auch Zählschleife) eine feste Anzahl an Wiederholungen durchlaufen. Eine Zählvariable i wird bspw. von 0 bis 6 in 1er Schritten gezählt. In Java programmiert man:
for(int i = 0; i < 7; i = i + 1){
System.out.println(i);
}
Die for-Schleife besitzt einen Schleifenkopf mit Initialisierung (Startwert), Bedingung (Abbruch) und Änderung (Schrittweite) und einen Schleifenkörper, der hier 7mal, mit Ausgabe der Zählvariable, wiederholt wird.
Inkrementieren und Dekrementieren Änderung des Variablenwertes

Diese Geschichte hat LIME seinen Namen gegeben: Möchte man den Wert einer Variable um eins erhöhen schreibt man:
i=i+1, möchte man ihn um eins verringern i=i-1.
Mathematisch ist dies nicht sinnvoll, aber
beim programmieren sehr wohl. Man stelle sich als Variable eine Glasschütte vor, deren Inhalt 3 Limetten sind. Möchte man
die Anzahl um eins erhöhen legt man eine dazu. Man nimmt also den alten Wert und erhöht diesen, so dass der neue Wert
4 Limetten sind.
Programmierer kürzen gerne ab:
i=i+1 | i++ oder i+=1 | ++i Inkrementieren
i=i-1 | i-- oder i-=1 | --i Dekrementieren
Aufgabe 1 Inkrementieren, Dekrementieren und Kurzschreibweisen

- Nenne eine alternative Schreibweise für
i=i+1,x++,y-=2,n*=2.
In einem Café gewährt der Inhaber folgenden Treuevorteil: Für jede 5 EUR bekommt man einen Treuestempel. Für 10 Stempel erhält man einen Rabatt im Wert von 3 EUR.
- Schreibe die Klasse
Treuestempel. Der Nutzer gibt den Einkaufswert ein. Berechnet und ausgegeben wird der Endpreis. Nutze Kurzschreibweisen. - Nutze eine for-Schleife mit der die Abfrage 3mal wiederholt wird.
- Simon kauft Kuchen im Wert von 46 EUR. Beurteile die folgende Aussage: "Er sollte für 4 EUR mehr einkaufen, dann spart er Geld."
- Schreibe einen Darlehensrechner. Der Nutzer gibt die Darlehenshöhe, die Zinshöhe und die anfängliche Tilgung ein.
i++,x+=1,y=y-2,n=n*2einkaufswert-=rabatt;for(int i=0; i<3; i++)- Er spart kein Geld, er zahlt 1 EUR mehr, sichert sich aber einen Rabatt und bekommt so mehr für sein Geld.
- Hinweis: Zinsen werden aufs Jahr berechnet und dann durch 12 geteilt. Die monatliche Tilgung reduziert die Restschuld monatlich. Dadurch werden die Zinszahlungen jeden Monat weniger und die Tilgung steigt.
Aufgabe 2 Welche Aussage ist wahr?
Wähle die korrekten Aussagen aus.
for(int i=0; i!=10; i=i+1) System.out.print(i+" ");Gib die Ausgabe an. Wähle eine Antwort.
- 0 1 2 3 4 5 6 7 8 9
- 0 1 2 3 4 5 6 7 8 9 10
- 1 2 3 4 5 6 7 8 9 10
- 1 2 3 4 5 6 7 8 9
for(int j=1; j<=15; j=j+3) System.out.print(j+" ");Gib die Ausgabe an. Wähle eine Antwort.
- 1 3 6 9 12 15
- 0 1 2 3 4 5 6 7 8 9 10
- 1 2 3 4 5 6 7 8 9 10 11 12 13
- 1 4 7 10 13
for(double k=0; k<3; k=k+0.5) System.out.print(k+" ");Gib die Ausgabe an. Wähle eine Antwort.
- 0.5 1.0 1.5 2.0 2.5 3.0
- 0 1 2
- 0 0.5 1.0 1.5 2.0 2.5
- 1 4 7 10 13
for(int l=10; l>0; l--) System.out.print(l+" ");Gib die Ausgabe an. Wähle eine Antwort.
- 10 9 8 7 6 5 4 3 2 1
- 9 8 7 6 5 4 3 2 1 0
- 10 8 6 4 2 0
- 10 9 8 7 6 5 4 3 2 1 0
for(int i=0; i<=10; i++) System.out.print(i+++" ");Gib die Ausgabe an. Wähle eine Antwort.
- 0 2 4 6 8 10
- 0 1 2 3 4 5 6 7 8 9 10
- 1 3 5 7 9
- 1 4 7 10 13
int i;
for(i=0; i<=10; i++) System.out.print(++i+" "); System.out.print(i); Gib die Ausgabe an. Wähle eine Antwort.
- 0 2 4 6 8 10
- 0 1 2 3 4 5 6 7 8 9 10
- 1 3 5 7 9 11 12
- 1 3 5 7 9 11
Verschachtelte for-Schleife Schleifen in Schleifen

Man kann for-Schleifen auch Verschachteln:
int i, j;
for(i = 0; i < 2; i++){
for(j = 0; j < 3; j++){
}
}
In diesem Beispiel wird die innere Schleife 3mal und die äußere Schleife 2mal durchlaufen, das macht insgesamt: 2 . 3 = 6mal.
Aufgabe 3 Exakte Zeiten mit verschachtelten for-Schleifen
Autoren: D. Supper
Wir trainieren unser Programmierkenntnisse mit verschachtelten Schleifen.
- Gib die Gesamtanzahl der Schleifendurchläufe an.
for(i=1;i<=10;i++){
for(j=0;j<10;j++);
};- 110mal
- 100mal
- 90mal
- 80mal
- Gib die Gesamtanzahl der Schleifendurchläufe an.
for(x=3;x<=10;x++){
for(y=10;y>5;y--);
}- 100mal
- 56mal
- 48mal
- 40mal
- Schreibe die Klasse
Zeitendie einen Countdown von 10 bis 0 zählt. Die Verzögerungszeit soll exakt 1 s betragen. Verwende dazu verschachtelte for-Schleifen und die Variablezeit = 10. - Für Profis : Schreibe die Klasse
VariableZeitenbei der mit Hilfe einer weiteren for-Schleife die Wartezeit zwischen 200 ms und 700 ms variiert wird.
Entspann dich erstmal ...
"Ein Netz hat Löcher, immer. Sonst wäre es ja eine Decke."
"Deswegen heißt es, zumindest in Deutschland, ja auch Mobilfunknetz und nicht Mobilfunkdecke." mademyday.com

Aufgabe 4 Finde den Fehler
Autoren: G. Kompa, D. Supper
for(int i=1;i<=10;i++){
System.out.println("Ich zähle" + i);
}
System.out.println("Ich zähle nicht" + i);
for(double j=0; j!=2.0; j+=0.1){
System.out.printf("%f \n",j);
}
Finde die Fehler.
Finde in der ersten Schleife heraus, wie auch der Wert außerhalb der Schleife angegeben werden kann.
Bei der zweiten Schleife lass 10 Nachkommastellen anzeigen.
Aufgabe 5 Schaltjahre
Autoren: G. Kompa, D. Supper

In unserem Kalender sind zum Ausgleich der Jahreslänge in regelmäßigen Abständen Schaltjahre eingebaut. Ein astronomisches Jahr hat dabei 365,24219 Kalendertage. Zur exakten Festlegung der Schaltjahre dienen folgende Regeln:
- Ist die Jahreszahl durch 4 teilbar, so ist das Jahr ein Schaltjahr. Diese Regel hat allerdings eine Ausnahme:
- Ist die Jahreszahl durch 100 teilbar, so ist das Jahr kein Schaltjahr. Diese Regel hat allerdings wiederum eine Ausnahme:
- Ist die Jahreszahl durch 400 teilbar, so ist das Jahr doch ein Schaltjahr.
- Gib eine Liste mit den Schaltjahren von 2000 - 2100 aus.
- Gib eine Liste mit allen Schaltjahren von Regeln 2 und 3 aus.
- Gib eine Liste aller Primzahlen bis 100 aus.
for(int i=2000; i<=2100; i=i+4){
...
Aufgabe 6 Mathe und ASCIIArt
Autoren: D. Supper | binnendifferenziert
- Schreibe die Klasse
Mittelwert: Deren Aufgabe besteht darin, eine bestimmte Anzahl von Werten über die Tastatur einzulesen. Die Summe der Werte soll berechnet und zusammen mit dem Mittelwert ausgegeben werden.Frage zuerst ab wie viele Werte der Benutzer eingeben möchte. Mit der Anzahl der Werte schreibst du dann die Bedingung der for-Schleife.
- Addiere nur gerade Zahlen.
- Für Mathefreaks: Berechne n!
- Für Honigfreaks: Zeichne eine Honigwabe in der Klasse
Honigwabe. - Zeichne ein ASCII-Art mit Hilfe einer for-Schleife in der Klasse
ASCIIArt.

System.out.printl("Wie viele Werte wollen sie eingeben?";
int anzahl = keyboard.nextInt();
for(int i=0; i<anzahl; i++){ ...if(wert%2== ...- Tip: Fakultät ist eine Matheoperation.
- Tip: Nutze eine for-Schleife und gib die entsprechenden Zeichen aus. Beachte das Backslash nur mit der Escapesequenz \\ dargestellt werden kann.
- Tip: Nutze das Internet zur Recherche.
Aufgabe 7 Pythagoreisches Tripel
Autoren: D. Supper | binnendifferenziert
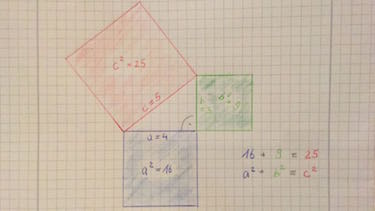
Drei ganzzahlige Längen, die die Seitenlängen eines rechtwinkligen Dreiecks darstellen, nennt man pythagoreisches Tripel. Es muss die Gleichung gelten, dass die Summe der Quadrate der beiden Seiten, welche an den rechten Winkel angrenzen, gleich dem Quadrat der Hypotenuse ist. (Satz des Pythagoras)
Erstelle die Klasse PythagoresischesTripel. Ermittle für die Variablen a, b, und c alle passenden Werte im Bereich für a, b, c von 1 bis 100.
Beispiel für ein Tripel: (3,4,5), da 3² + 4² = 5².
Benutze dafür eine dreifach verschachtelte for-Schleife, die die möglichen Werte durchläuft. Stelle sicher, dass kein Tripel doppelt vorkommt.
(9,12,15) (9,40,41) (10,24,26) (11,60,61) (12,16,20)
(12,35,37) (13,84,85) (14,48,50) (15,20,25) (15,36,39)
(16,30,34) (16,63,65) (18,24,30) (18,80,82) (20,21,29)
(20,48,52) (21,28,35) (21,72,75) (24,32,40) (24,45,51)
(24,70,74) (25,60,65) (27,36,45) (28,45,53) (28,96,100)
(30,40,50) (30,72,78) (32,60,68) (33,44,55) (33,56,65)
(35,84,91) (36,48,60) (36,77,85) (39,52,65) (39,80,89)
(40,42,58) (40,75,85) (42,56,70) (45,60,75) (48,55,73)
(48,64,80) (51,68,85) (54,72,90) (57,76,95) (60,63,87)
(60,80,100) (65,72,97)
Aufgabe 8 Das Einmaleins
Autoren: D. Supper | binnendifferenziert
Schreibe die Klasse Einmaleins: Deren Aufgabe besteht darin, das kleine Einmaleins in tabellarischer Form zu erzeugen.
Für die Tabelle müssen insgesamt hundert Zahlen gedruckt werden. Das lässt vermuten, dass eine Schleife sinnvoll wäre. Die Tabelle ist aber aus zehn Zeilen mit jeweils zehn Spalten aufgebaut. Mit anderen Worten, es müssen insgesamt zehn Zeilen gedruckt werden und in jeder Zeile wiederum zehn Zahlen. In diesem Fall bietet sich eine geschachtelte Zeile zur Erzeugung der Tabelle an.

for (int i = 1; i <= 10; i++) {
for (int j = 1; j <= 10; j++) {
System.out.printf("%3d•%d = %2d ",i,j,(i*j));
}
System.out.println();
}
Wortliste und Satzbausteine
| die for-Schleife, -en | Die for-Schleife (auch Zählschleife) wiederholt einen Anweisungsblock x-mal. Dabei wird ein Startwert festgelegt, eine Abbruchbedingung und die Schrittweite |
| die Initialisierung, -en | hier wird der Startwert festgelegt, z.B. i = 0 |
| die Abbruchbedingung, -en | Sobald die Bedingung den Wert false ergibt wird die Schleife verlassen, z.B. i < 10 |
| die Änderung, -en | hier wird die Schrittweite festgelegt, z.B. in 1er Schritten (i = i + 1) |
| die Zählvariable, -en | Variable, welche zum zählen in der for-Schleife verwendet wird |
| inkrementieren | i = i + 1 kurz i++ oder i = i + 5 |
| dekrementieren | i = i - 1 kurz i-- oder i-=1 |
| verschachtelte for-Schleife | eine for-Schleife in einer anderen for-Schleife |