line diagram AC

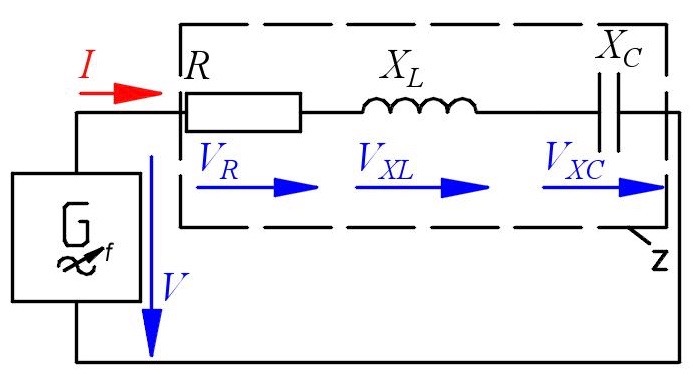
Alternating Current Series Circuits

In the series circuit, the total voltage is the sum of the partial voltages. Due to the phase shift between reactive and real voltage, these must be added geometrically.

1 AC series circuit
pawns in a game

Since in the series circuit the resistances and powers behave like the voltages the geometrical addition applies to them as well.

On this page, various tasks for the AC series are presented and the calculation path is explained. In addition, all relevant formulas are listed.

2 RC series circuit
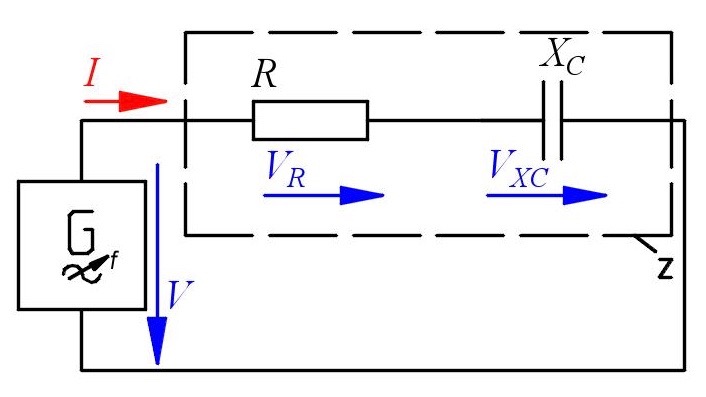
AC RC series circuit
pointer diagramm

The real voltage $V_R$ is geometrically ad­ded to the capaciti ve reactive voltage $V_{XC}$ in order to obtain the apparent voltage $V$. With a phase shift of $\varphi\hspace{-1mm}=\hspace{-1mm} 90°$ the values can be calculated as follows:

$V=\sqrt{V_R^2+V_{X}^2}$

$V_R=V\cdot cos\varphi$

$V_{X}=V\cdot sin\varphi$

3 RL series circuit
AC RL series circuit
pointer diagramm

Since the resistances behave like the voltages, the resistance $R$ is geometrically added to the reactance $X$ in order to obtain the impedance $Z$. With a phase shift of $\varphi = 90\:°$ we can write:

$Z=V/I=\sqrt{R^2+X^2}$

$R=V_R/I=Z\cdot cos\varphi$

$X=V_{X}/I=Z\cdot sin\varphi$

4 RLC series circuit
AC RLC series circuit
pointer diagramm

The real power $P$ is geometrically added to the reactive power $Q$ in order to obtain the apparent power $S$. With a phase shift of $\varphi = 90\:°$ we can write:

$S=V\cdot I=\sqrt{P^2+Q^2}$

$P=V_R\cdot I=S\cdot cos\varphi$

$Q=V_{X}\cdot I=S\cdot sin\varphi$

5 reactive power
line diagram reactive power

Reactive power does not effect the power consumption of the load. Every 5 ms (positive power) the load dissipates the power, the other 5 ms (negative power) the load generates the power and will send it back to the power plant.

Nevertheless the power plant has to provide the electric power which will be additional load for the transmission line. So the power dissipation occurs mainly at the transmission line.

Therefore the power suppliers are not interested in reactive load and will ask you to pay for it if you do not compensate.

6 resonant circuit
RLC-circuit

A RLC-circuit can be a resonant circuit if the two reactances are equal, $X_L=X_C$.

$$f_r = \frac{1}{2\pi \sqrt{L C}}$$

Once charged, the capacitor is charged and discharged all the time. While discharging, the current in the inductance changes, thus building up a magnetic field. As long the current flow is positive the magnetic field will be build up and the voltage $V_{XC}$ will fall. When the capacitor is discharged the whole energy is stored in the magnetic field.

7 stored energy in a resonant circuit
RLC-circuit

If the magnetic field collapses the induced voltage will charge the capacitor again. As long as the current flow is negative, the capacitor will be charged and the voltage $V_{XC}$ will rise. The energy is stored in the electric field.

$$\frac{1}{2}LI_{max}^2=\frac{1}{2}CV_{max}^2$$

ideas of
G. Vogt, Elektronikschule Tettnang
J. Grehn, J. Krause, "Metzler-Physik", Schroedel Verlag, 2002



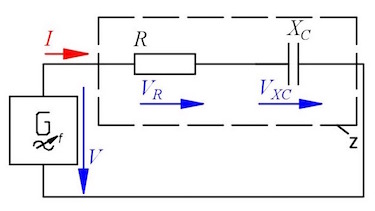
Question 1 RC circuit

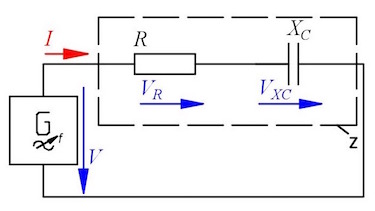
RC-circuit

In a series circuit with capacitor and resistor the voltages are measured as follows: VR = 5.21 V and VXC = 3.22 V. The resistance is R = 220 Ω and the frequency f = 250 Hz.

  1. Construct and calculate the voltage V.
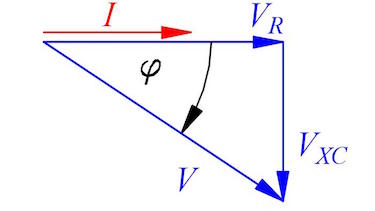
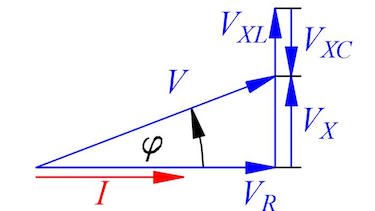
  2. Construct and calculate the phaseshift φ.
  3. Determine the current $I$ and the impedance Z.
  4. Calculate the reactance XC and the corresponding capacity C.
  5. Calculate the real power P, the reactive power Q and the apparent power S.
  1. voltage $V=\sqrt{V_R^2+V_{XC}^2}=6.12\:V$
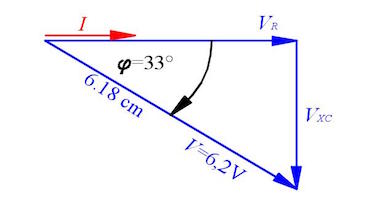
    pointer diagram
  2. phaseshift $\varphi=32.97\:°$
  3. current $I=\frac{V_R}{R}=23.7\:mA$
    impedance $Z=\frac{V}{I}=258.23\:\Omega$
  4. reactance $X_C=\frac{V_{XC}}{I}=135.9\:\Omega$
    capacity $C=\frac{1}{2\pi f X_C}=4.68\:\mu F$
  5. real power $P=123.5\:mW$
    reactive power $Q=76.3\:mW$
    apparent power $S=145\:mW$


Question 2 vocabulary

Find the correct answers.

  1. What is the reactance?


  2. 200 Ohm is ...


RC-circuit
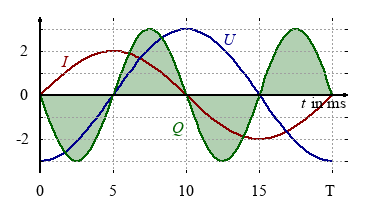
line diagram reactive power

  1. Reactive power causes energy loss ...


  2. The power consumption is affected by...




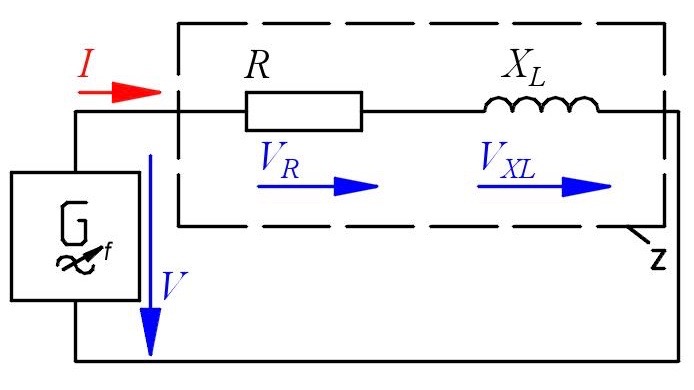
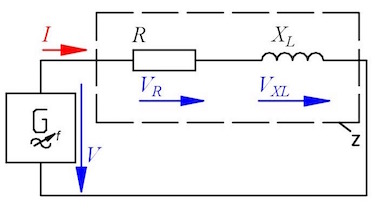
Question 3 RL circuit

In a series circuit with inductor and resistor the following values are known: L = 550 mH, f = 50 Hz, V = 230 V and R = 470 Ω.

  1. Calculate the reactance XL,
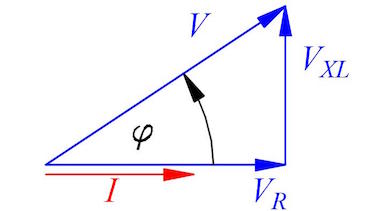
  2. Construct the impedance Z and phaseshift φ.
  3. Calculate the impedance Z and phaseshift φ.
  4. Calculate the current I.
  5. Calculate the real voltage VRand the reactive voltage VX.
  6. Calcultate the real power P, the reactive power Q and the apparent power S.
RL-circuit

  1. reactance $X_L=172,8\:\Omega$
  2. impedance $Z$ and phaseshift $\varphi$
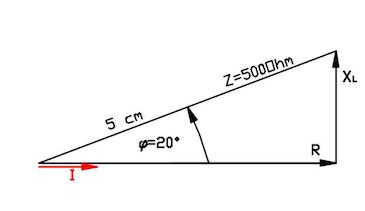
    pointer diagram
  3. impedance $Z= 500\:\Omega$ and phaseshift $\varphi=20.2\:°$
  4. current $I=V/Z=459\:mA$
  5. real voltage $V_R=215\:V$ and reactive voltage $V_X=79.4\:V$
  6. real power $P=98.2\:W$, reactive power $Q=36.5\:W$ and apparent power $S=105.7\:W$


First relax ...

Here you can find out something about the power of resonance.

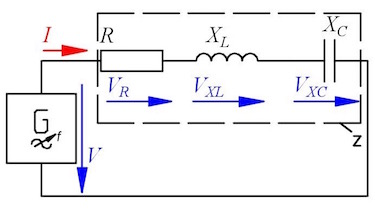
Question 4 RLC-circuit

In the circuit is R = 2 kΩ, XL = 3 kΩ, XC = 4 kΩ, the current I = 2 mA and the frequency f = 50 Hz.

  1. Determine by drawing and calculating the impedance Z and phase shift φ.
  2. Calculate the voltages V, VXC, VXL and VX.
  3. Calculate the inductivity L and capacity C.
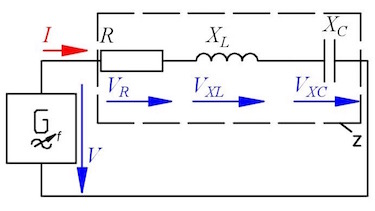
RLC-circuit

  1. reactance $X=1\:k\Omega$,
    impedance $Z=2.24\:k\Omega$
    phase shipf $\varphi = 26.56\:°$
    pointer diagramm
  2. voltage $V=Z\cdot I= 4.48\:V$
    real voltage $V_R=4\:V$,
    inductive voltage $V_{XL}=6\:V$,
    capacitive voltage $V_{XC}=8\:V$,
  3. inductivity $L=9.5492\:H$
    capacity $C=7.9\cdot 10^{-7}\:F$

Question 5 RLC-circuit

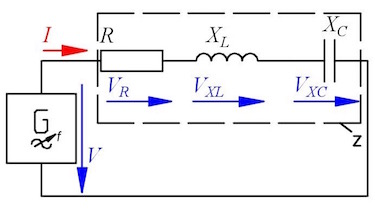
RLC-circuit

In the circuit is R = 250 Ω, L = 191 mH, the voltage V = 10 V and the frequency f = 500 Hz.

  1. Calculate the current I when the voltage across the resistor and inductive reactor is 5 V.
  2. Determine the capacitive voltage VXC and the capacitance C.
  3. Which frequency f is nescesarry to get the maximum current? Calculate the resulting voltage across the resistor and inductive reactor.
  4. Which voltage will you measure across the inductor for f → ∞ and f → 0?
  1. inductive reactance $X_L=600\:\Omega$,
    impedance $Z_{RX_L}=650\:\Omega$,
    current $I=\frac{5\:V}{650\:\Omega}=7.69 mA$.
  2. real voltage $V_R=1.925\:V$,
    inductive voltage $V_{XL}=4.62\:V$,
    capacitive voltage $V_{XC}=\sqrt{V-V_R^2}+V_{XL}=14.43\:V$,
    capacitive reactance $X_C=1874.3\:\Omega$,
    capacitance $C=169.83\:nF$.
  3. resonance frequency $f_R=883.24\:Hz$,
    real voltage $V_R=V=10\:V$,
    current $I=40\:mA$,
    inductive voltage $V_{XL}=42.4\:V$,
    voltage across the resistor and inductive reactor $V_{RX_L}=43.56\:V$
  4. inductive voltage for f → ∞: $V_{XL}=10\:V$,
    inductive voltage for f → 0: $V_{XL}=0\:V$

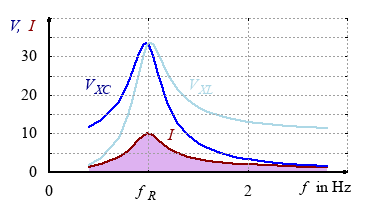
Question 6 resonant circuit

In a RLC-circuit a capacitor is charged and then the circuit closed. The resonance frequency is 1 Hz and the inductance 3.37 H. The maximum voltage is 1.48 V.

  1. Describe the energy transfer between inductor and capacitor.
  2. Draw the line diagram of VXC and current I.
  3. Calculate the capacitance C.
  4. Calculate the maximum current in the resonant circuit.
  5. Calculate the new resonant frequency if the area of the capacitor is half as much as before.
  6. Describe why the reactive voltage can be higher than the applied voltage during resonance.
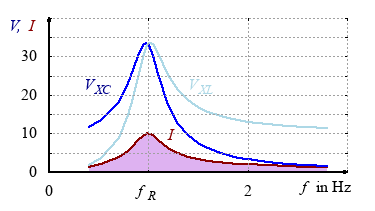
resonance of voltages and current

  1. energy transfer:
    Once charged, the capacitor is charged and discharged all the time. While discharging, the current in the inductance changes, thus building up a magnetic field. As long the current flow is positive the magnetic field will be build up and the voltage $V_{XC}$ will fall. When the capacitor is discharged the whole energy is stored in the magnetic field.
    If the magnetic field collapses the induced voltage will charge the capacitor again. As long as the current flow is negative, the capacitor will be charged and the voltage $V_{XC}$ will rise. The energy is stored in the electric field. $$\frac{1}{2}LI_{max}^2=\frac{1}{2}CV_{max}^2$$
  2. line diagram of VXC and current I
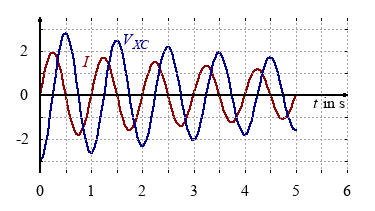
    line diagram voltage and current
  3. capacitance $C = \frac{1}{4\pi^2 f_r^2L} = 7.52\:mF$
  4. stored energy: $\frac{1}{2}LI_{max}^2=\frac{1}{2}CV_{max}^2$
    maximum current: $I_{max}=\sqrt{\frac{C}{L}}\cdot V_{max}=0.07\:A$
  5. capacitance: $C=7.52/2=3.76\:mF$,
    resonant frequency: $f = \frac{1}{2\pi \sqrt{LC}} = 1.425\:Hz$
  6. Since the resonant current is only determinded by applied voltage and resistance, but the reactance by capacitance, inductance and frequency, the reactive voltage rises with the current.
© mylime.info