mylime - Physik

1 Thermionic emission and deflection

The low voltage of 6 V heats the cathode, so electrons can escape the surface by thermionic emission. The cylindrical positive anode with a voltage of $V=3000\:\text{V}$ attracts the electrons with charge $e=1.6\cdot 10^{-19}\:\text{C}$ and mass $m=9.1\cdot 10^{-31}\:\text{kg}$. Electrons which pass the cylindrical anode will form an electron beam. The loss in electrical potential energy is gained in kinetic energy:

$$eV=0.5mv^2$$

Note: For the energy the unit eV (electron-volt) is often used: $1\:\text{eV}=1.6\cdot 10^{-19}\:\text{J}$.
The deflective force $F$ is caused by electric field with $V=2000\:V$ and distance $d$ of the metal plates: $F=e\cdot V/d= am$

2 Millikan's experiment to measure electron charge

1923 Robert Millikan got the nobel prize in physics for determine the elementary charge of an electron $e=1.602\cdot 10^{-19}\:\text{C}$. The experimental aperture consists of a parallel pair of horizontal metal plates with electrically charged oil drops in between. Millikan focussed on one drop and adjusted the voltage until the drop was stationary between the two plates. For this drop, its weight is equal to the electric force.

$$mg=QE=Q\frac{V}{d}$$

$m = \rho_{oil} \cdot V=\rho_{oil} \cdot 4/3\cdot \pi \cdot r^3 $: mass of the droplet, $g$: gravitational acceleration, $r$: radius of the spherical oil drop and $d$: distance between the metal plates.

3 Millikan's experiment to measure electron charge

If the radius of an oildrop is not known one can measure the terminal velocity of the drop without the electric field. The weight of the oil drop is equal to the viscous drag forces at terminal velocity. The viscous drag forces obey stoke's law.

$$\rho_{oil}\cdot \frac{4}{3}\pi r^3\cdot g=6\pi \eta rv$$

The viscosity of air is $\eta=17.1\cdot 10^{-6}\:\text{kg/(ms)}$, $v$ is found by timing the drop falling. With the determined radius we repeat Milikan's experiment several times. Then the charge is always a multiple of $-1.62\cdot 10^{-19}\:\text{C}$, the elementary electron charge. Thomson's experiment gives us even the electron mass $m_e=9.1\cdot 10^{-31}\:\text{kg}$.

4 Photo-electric effect

There are free emitted electrons (photo-electrons) through light. The light gives the electrons the energy to escape the metal.

Brighter violet light causes more emitted electrons. Therefore one can observe a higher current. Nevertheless if we use dim or bright red light there is no current at all.

Light is made of tiny particles, quantums, called photons. Each photon has a certain energy level. Planck derived the photons energy $E_{ph}$ in dependence of the wavelength $\lambda$ and the Planck constant $h=6.6\cdot 10^{-34}\:\text{Js}$. Planck's equation:

$$E_{ph}=h\cdot f = h\cdot \frac{c}{\lambda}$$

5 The work function

frequency of light versus kinetic energy of photoelectrons

Photons carry energy and the energy depends on color, i.e. frequency and not on its intensity. If the frequency is not high enough it won't be able to liberate electrons.

With the retarding potential method we illuminate a cathode with different frequencies of light. If electrons are liberated we increase the retarding voltage until the photocurrent is zero. The retarding voltage $V$ is proportional to the kinetic energy $E_{\text{kin}}=e\cdot V$. Light of frequencies below the threshold frequency $f_0$ does not give any electrons. The gradient is the planck's constant $h$, the y-intercept is the energy needed to escape from the metal, the work function $\Phi$ with Einstein's equation:

$$E_k=hf-\Phi$$

6 X-ray spectra

X-rays (X-radiation) are electromagnetic waves. They are produced when high-speed elctrons with an energy starting from $30\:$keV decelarate quickly. The freqency range is from $3\cdot 10^{16}\:$Hz to $3\cdot 10^{19}\:$Hz, with a corresponding wavelength of $0.01\:$nm to $10\:$nm. The total kinetic energy of the electrons is transformed to X-radiation if:

$$E_{kin}=eV=hf_{max}=hc/\lambda_{min}$$

continuous x-ray spectrum: Electrons are scattered on atoms, some loosing their total incident kinetic energy ($\lambda_{min}$), some only partly to X-ray photons.

characteristic x-ray spectrum: The electrons collide with an atom of the target knocking out one of the most internal electrons of the atom.

Question 1 Millikan's experiment

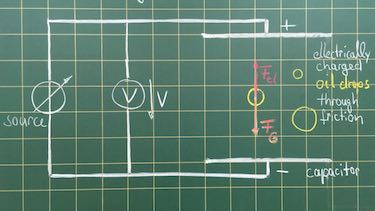
A negatively charged oil drop with unknown mass is observed between two horizontal parallel metal plates with the distance $d=12\:mm$ in Millikan's experiment. The droplet falls vertical at its terminal speed. By timing 1 minute, the drop falls 1 cm. The viscosity of air is $\eta_{air}=17.1\cdot 10^{-6}\:kg/(ms)$. The density of the oil is $\rho=855\:kg/m^3$.

Calculate the terminal speed of the droplet.
Derive an expression for the radius $r$ of the droplet in terms of $v$, $\eta_{air}$, $\rho_{oil}$, $g$ and calculate the radius.
Calculate the mass of the oil droplet from the radius and other relevant data.

If two forces balance, the oil drop is held stationary.

What are the two forces acting on the drop and in which direction do they act?
Derive the equation for the force balance.
Calculate the necessary voltage to hold the oil drop stationary, if the charge on the oil drop is a multiple of $e$.
Decide whether or not you can hold the oil drop stationary with 19 V.

terminal speed $v=1/6000 m/s$
radius of the spherical droplet $r=\sqrt{\frac{6\pi \eta v}{\rho_{oil}4/3 \pi g}}=1.24\cdot 10^{-6}\:m$
mass of the oil droplet $m=6.83\cdot 10^{-14}\:kg$
The two forces $F_G$ and $F_{el}$ are acting contrarious.
force balance: $F_G=F_{el}$ $\Leftrightarrow mg=Q\frac{V}{d}$

voltage to hold the oil drop stationary $V=\frac{mgd}{Q}$

$Q$	$e$	$2e$	$3e$	$4e$
$V$ in V	5	10	15	20

Since $Q$ is a multiple of $e$ the oil drop can not be held stationary with 19 V.

Question 2 retarding potential method

Author: J. Blum, D. Supper, CDSC

The retarding potential method is used to determine Planck's constant $h$.

Draw the circuit of the experiment and explain how to execute the experiment.

Determine with the following experimental data Planck's constant $h$ and the work function $\Phi$.

color	$f$ in $10^{14}\:$Hz	voltage in V
yellow	5.19	0.15
green	5.5	0.3
blue	6.88	0.9
violet	7.41	1.1

Determine the threshold frequency $f_0$ of light which is able to liberate electrons.

Light of wavelength $\lambda=230\:\text{nm}$ liberates electrons out of a metal with the maximum energy of $1.8\:$eV. Calculate the work function $\Phi$ and threshold frequency $f_0$ for this metal.
Light of wavelength $\lambda=360\:\text{nm}$ liberates electrons out of cesium with the a work function $\Phi=1.94\:\text{eV}$. Calculate the kinetic energy and the speed of the fastest photoelectrons.
The work function for various elements is given as follows:

element Ag Cu Al Si

$\Phi$ in eV 4.7 4.48 4.2 3.59

Calculate the threshold frequency $f_0$ and the corresponding cut-off wavelength $\lambda_0$ for each element.

If electrons are liberated we increase the retarding voltage until $I=0\:\text{A}$. Different colors do have different voltages and all measuring points are on a straight line with the gradient $m=h$.
Planck's constant: $h=\frac{\Delta E}{\Delta f} \approx 6.9 \cdot 10^{-34}\:\text{Js}$
work function $\Phi=hf-E \approx 1.92\:\text{eV}$
threshold frequency $f_0$: $h\cdot f_0-\Phi=0$ $\Leftrightarrow f_0=\frac{\Phi}{h}=\frac{1.96\:eV}{6.6\cdot 10^{-34}\:Hz}$ $=4.81\cdot 10^{14}\:\text{Hz}$
frequency $f=\frac{c}{\lambda}=\frac{300\cdot 10^{6}}{230\cdot 10^{-9}}$ $=13.04\cdot 10^{14}\:\text{Hz}$
work function $\Phi=hf-E = 5.31-1.8$ $=3.51\:\text{eV}$
threshold frequency $f_0=\frac{\Phi}{h}=\frac{3.51\:eV}{6.6\cdot 10^{-34}\:Hz}$ $=8.62\cdot 10^{14}\:\text{Hz}$
frequency $f=\frac{c}{\lambda}=\frac{300\cdot 10^{6}}{360\cdot 10^{-9}}$ $=8.33\cdot 10^{14}\:\text{Hz}$
kinetic energy $E_{kin}=hf-\Phi=1.45\:eV$ $=2.355 \cdot 10^{-19}\:\text{J}$
speed of the fastest electron $v=\sqrt{2E_{kin}/m}$ $=\sqrt{2\cdot 2.36 \cdot 10^{-19}/0.1 \cdot 10^{-31}}$ $=719432\:\text{m/s}$.

threshold frequency $f_0=\Phi/h$
cut-off wavelength $\lambda_0=c/f_0$

element	Ag	Cu	Al	Si
$\Phi$ in eV	4.7	4.48	4.2	3.59
$f_0$ in $10^{14}$ Hz	11.5	11.0	10.3	8.81
$\lambda_0$ in nm	261	273	291	340

Experiment 1 Determining Planck’s Constant with LEDs

Materials:

LEDs: red, yellow, green and blue. Choose LEDs without coloured housing.
10 V adjustable voltage source
two multimeters for voltage and current
1 kΩ potentiometer

Procedure:

Set up the circuit as shown in the figure. Be careful: Do not apply to high current, this will destroy the LEDs.
Apply voltage, measure the current for each color. When the threshold is reached change the voltage in steps of 0.05 V.
For each color, plot a graph of current versus voltage. On each graph, fit a straight line in order to find out the threshold voltage $V_{th}$ for each individual LED.
Find out from the datasheet the wavelength of each LED, calculate the corresponding frequency and plot the energy $eV_{th}$ versus the frequency. Calculate the gradient.
Calculate the theoretical energy.

color	blue	green	red
wavelength $\lambda$ in nm	465	...	...
frequency $f$ in $10^{14}$ Hz	...	...	...
$E=eV_{th}$	...	...	...

possible experimental values:

color	blue	green	yellow	red	dark red	infrared
wavelength $\lambda$ in nm	465	560	585	635	660	950
frequency $f$ in $10^{14}$ Hz
$E=eV_{th}$ in $eV$	2.7	1.69	1.62	1.51	1.51	1.1

Question 3 energy of photons

Calculate the energy of the photons in $eV$ and $J$ for the following electro-magnetic radiation:

radio $\lambda=3\:m$
Wi-fi $\lambda=125\:mm$
red light $\lambda=630\:nm$
blue light $\lambda=430\:nm$
X-rays $\lambda=1 \cdot 10^{-8}\:m$
cosmic rays $\lambda=1\cdot 10^{-16}\:m$

radio $E=6.6 \cdot 10^{-26}\:J= 412\:neV$
Wi-fi $E=1.58 \cdot 10^{-18}\:J= 9.9\:\mu eV$
red light $E=3.14 \cdot 10^{-19}\:J= 1.96\:eV$
blue light $E=4.60 \cdot 10^{-19}\:J= 2.87\:eV$
X-rays $E=1.98 \cdot 10^{-17}\:J= 23.6\:eV$
cosmic rays $E=1.98 \cdot 10^{-9}\:J$ $= 1.2\cdot 10^{10}\:eV$

Question 4 X-rays

After thermionic emission electrons are accelerated with $30\:keV$ and $50\:keV$ hitting the target.

Determine the cutoff wavelength $\lambda_{min}$ for the two potentials.
Calculate the maximum speed of the electrons.
Describe the principle of production of X-rays.
Explain what is meant by continuous x-ray spectrum.

For measuring the different wavelength we use the Bragg grating with a LIF-crystal (lithium fluoride). The crystal has a grating constant of $d=2.014 \cdot 10^{-10}\:m$.

Describe and derive the Bragg equation $k \lambda = 2d \, \cos(\delta)$.
Calculate for constructive interference the different angles for the two cut-off wavelengths.

$30\:keV$: cutoff wavelength $\lambda_{min}=\frac{hc}{E}=0.0411\:nm$
$50\:keV$: cutoff wavelength $\lambda_{min}=\frac{hc}{E}=0.0247\:nm$
$\frac{1}{2}mv^2=h\frac{c}{\lambda_{min}}$ $\Leftrightarrow$
$30\:keV$: maximum speed $v=\sqrt{\frac{2hc}{m_e \lambda_{min}}}=102.9\cdot 10^{6}~\frac{m}{s}$
$50\:keV$: maximum speed $v=\sqrt{\frac{2hc}{m_e \lambda_{min}}}=132.7\cdot 10^{6}~\frac{m}{s}$
X-rays (X-radiation) are electromagnetic waves. They are produced when high-speed electrons ($>30\:keV$) decelarate quickly.
The continuous x-ray spectrum is produced when high speed electrons are scattered on atoms, some losing their total incident kinetic energy ($\lambda_{min}$), some only partly to X-ray photons.
Two rays with the identical wavelength are reflected at two different crystalline atoms. They will have at certain angle constructive interference. So for each wavelength we get a different angle. With the path difference $\Delta s=2d\cos (\delta)$ we obtain: $k \lambda = 2d \, \cos(\delta)$, with $k$ is a integer.
$30\:keV$ - $\lambda_{min}=0.0411\:nm$: $\delta=cos^{-1}\left(\frac{k \lambda}{2d}\right) = 84.14^\circ$
$50\:keV$ - $\lambda_{min}=0.0247\:nm$: $\delta=cos^{-1}\left(\frac{k \lambda}{2d}\right) = 86.48^\circ$

Terms and phrases

Thermionic emission	if a low voltage heats a cathode, electrons can escape the surface
electron-volt, eV	a energy unit for small particles: $1\:\text{eV}=1.6\cdot 10^{-19}\:\text{J}$.
Millikan's experiment	an experiment from Robert Millikan to determine the elementary charge of an electron $e=1.602\cdot 10^{-19}\:\text{C}$
photo-electric effect	free emitted electrons through light
Planck's equation	$E_{Ph}=h\cdot f$ with Planck's constant $h=6.6\cdot 10^{-34}\:\text{Js}
photon	Light is made of tiny particles, quantums called photons. Each Photon has a certain energy which can be calculated by Planck's equation.
Einstein's equation	The energy needed to liberate electrons from a metal surface is called the work function $\Phi$. The kinetic energy of the electron is calculated by the energy of the photon $hf$ with Einstein's equation: $E_{kin}=hf - \Phi$.

X-rays	X-rays (X-radiation) are electromagnetic waves. They are produced when high-speed electrons decelerate quickly. The frequency range is from $3\cdot 10^{16}\:$Hz to $3\cdot 10^{19}\:$Hz, with a corresponding wavelength of 0.01 to 10 nm.
Wilhelm Conrad Röntgen	German scientist who discovered in 1985 and named it X-radiation to signify an unknown type of radiation.
minimum wavelength of X-rays	The minimum wavelength or cutoff wavelength $\lambda_{min}$ corresponds to the maximum frequency $f_0$ of X-radiation
continuous x-ray spectrum	Electrons are scattered on atoms, some losing their total incident kinetic energy ($\lambda_{min}$), some only partly to X-ray photons.
characteristic x-ray spectrum	The electrons collide with an atom of the target knocking out one of the most internal electrons of the atom.

Photons and electrons