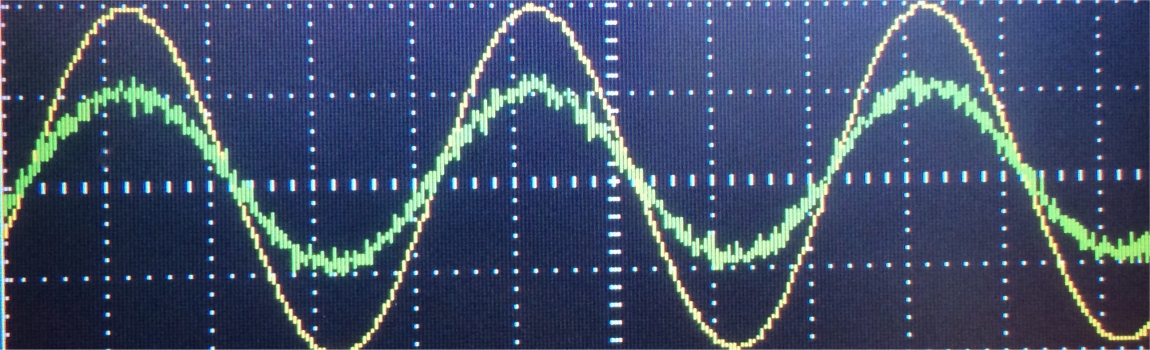
Alternating Current | AC
Line chart and pointer diagramm
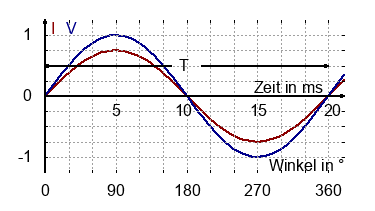
Alternating current (AC) changes its value and direction periodically. The arethmetic mean is zero. The current and voltage can be written as:
$$ v(t)=V_0 \cdot sin \left( \frac{2\pi}{T} \cdot t \right)$$ $$ i(t)=I_0 \cdot sin \left( \frac{2\pi}{T} \cdot t \right)$$$V_0$, $I_0$ is the peak value or amplitude (also $V_p$, $I_p$). The time for one complete circle is called the time period $T$. The frequency of the signal is $f=\frac{1}{T}$ with $[f]=\frac{1}{s}$.
The pointer with the length $V_p$ or $I_p$ is rotating anti-clockwise 50times per second. With this additional information, the pointer is an alternative diagram for alternating current.
The angular frequency $\omega$ is defined as:
$$\omega=2\pi f = \frac{2\pi}{T}$$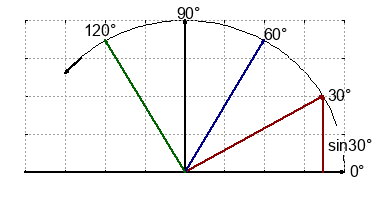
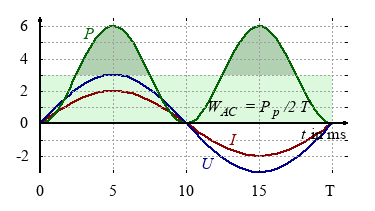
Root mean square | rms
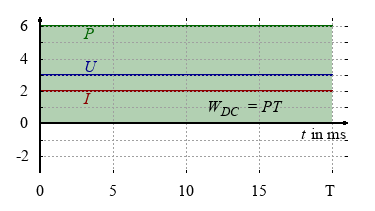
Just imagine you have to design an uninterrupted power supply (UPS) for illumination with car batteries. The peak voltage of the alternanting current is 325 V. How many 12 V batteries do you have to add in series in order to obtain the same brightness or power dissipation?
If we compare direct and alternating current: Which peak voltage is nescessary to obtain the same power dissipation in a resistor.
The root mean square, also known as quadratic mean, is equal to the value of a direct voltage or current, that would produce the identical power dissipation in a resistive load.
Resistor in AC circuits
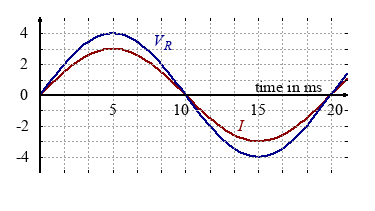
A sinusoidally voltage applied to a resistive load results in an alternating current that is in phase with the voltage.
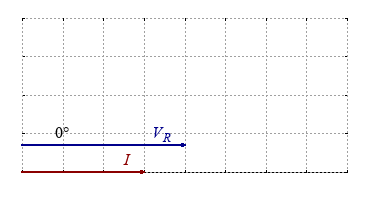
$$ V_R(t)=V_0 \cdot sin \left( \frac{2\pi}{T} \cdot t \right)$$ $$ I(t)=I_0 \cdot sin \left( \frac{2\pi}{T} \cdot t \right)$$The two pointers $V_R$ and $I$ are in phase, i.e. there is no angle between the two pointers.
Note that you can draw this two pointers in any direction, since they rotate anti-clockwise 50times per second. Nevertheless both must have the identical direction, since there is no phase shift between them.
Capacitor in AC circuits
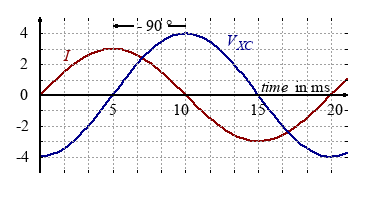
As one day my portable radio did not function properly, I started to repair it, since I wanted to take it with me to the beach. I discovered that a capacitor was completely darkened, so that the labeling could not be seen anymore at all. So I changed the capacitor on the off chance. The result: The low frequencies where cut off. But how could this happen?
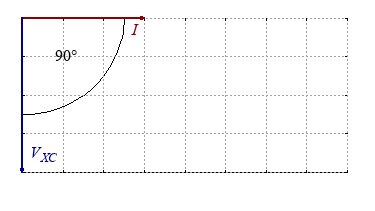
If we measure the voltage and current on a capacitor in an AC circuit one can observe a 90 degree phase shift between voltage and current. The capacitor is charged and discharged all the time. As long as the current flow is positiv, the capacitor will be charged and the voltage $V_X$ will rise.
chain of effects: I+ → Q↑ → VX↑
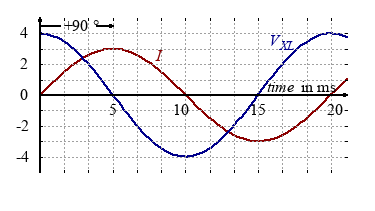
Since 90 degree correlates to 5 ms, the current and voltage can be written as:
$$ V_{XC}(t)=V_0 \cdot sin \left( \frac{2\pi}{T} \cdot (t-5) \right)$$ $$ I(t)=I_0 \cdot sin \left( \frac{2\pi}{T} \cdot t \right)$$Capacitance: the voltage lags the current.
We could also say: the current leads the voltage 90 degree in phase.
| $f$ in Hz | 50 | 100 | 200 | 500 |
| $V_X$ in V | 3.16 | 3.16 | 3.16 | 3.11 |
| $I$ in mA | 0.87 | 1.94 | 3.9 | 9.6 |
| $X_C$ in Ω | ... |
A capacitor with constant capacity of C = 1000 nF is examined in an AC circuit. Beside a voltage $V_X$ we can also measure a current $I$. So the capacitor acts in an AC circuit as a resitance. Calculate the resulting resistance $X_C$ and draw a frequency-reactance-diagramm..
Capacitors with different capacities and constant frequency f = 1000 Hz are examined in an AC circuit. Calculate the resulting capcitive reactance $X_C=\frac{V_X}{I}$ and draw a capacity-reactance-diagramm.
| $C$ in nF | 50 | 100 | 200 | 500 |
| $V_X$ in V | 3.16 | 3.15 | 3.15 | 3.10 |
| $I$ in mA | 0.93 | 1.98 | 4.1 | 9.1 |
| $X_C$ in Ω | ... |
The capacitve reactance $X_C$ is inversley proportional to frequency $f$ and capacitance $C$:
Inductor in AC circuits
Inductance: The voltage leads the current.
But we could also say: The current lags the voltage 90 degree in phase.
Since 90 degree correlates to 5 ms, the current and voltage can be written as:
$$ V_{XL}(t)=V_0 \cdot sin \left( \frac{2\pi}{T} \cdot (t+5) \right)$$ $$ I(t)=I_0 \cdot sin \left( \frac{2\pi}{T} \cdot t \right)$$The magnetic field in the inductance changes its direction all the time. As long as the voltage is positiv, the current and magnetic field will rise.
Chain of effects: VX + → I↑ → B↑
In the pointer diagramm we draw a 90 degree phase shift between current and voltge.
The inductive reactance $X_L$ is proportional to the inductance $L$ and frequency $f$:
$$X_{L} \sim f \:\:\:\: X_{C} \sim L$$ $$X_{L}=2 \pi fL=\omega L \: \: \: [X_L]=\frac{H}{s}=\Omega$$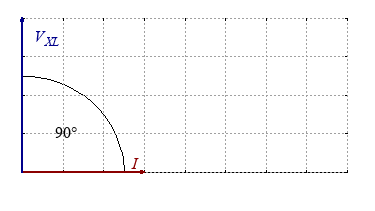
English and german Terms
| real power $P$ | Wirkleistung $P$ |
| reactive power $Q$ | Blindleistung $Q$ |
| apparent power $S$ | Scheinleistung $S$ |
| power factor $cos \varphi$ | Wirkleistungsfaktor $cos \varphi$ |
| reactive factor $sin \varphi$ | Blindleistungsfaktor $sin \varphi$ |
| real voltage $V_R$ | Wirkspannung $U_W$ |
| reactive voltage $V_X$ | Blindspannung $U_b$ |
| apparent voltage $V$ | Scheinspannung $U$ |
| resistance $R$ | ohmscher Widerstand $R$ |
| capcitive reactance $X_C$ | kapazitiver Blindwiderstand $X_{bC}$ |
| inductive reactance $X_L$ | induktiver Blindwiderstand $X_{bL}$ |
| impedance $Z$ | Scheinwiderstand $Z$ |