Atomic structure and energy levels
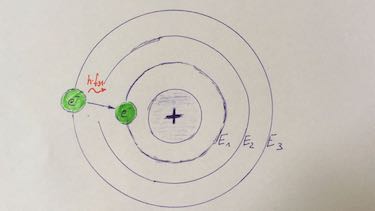
Question 1 atomic model
Which statement is correct?
Question 2 kinetic and potential energy of electrons in Hydrogen atom
| $m_e$ in kg | $9.1\cdot 10^{-31}$ |
| $e$ in As | $1.602\cdot 10^{-19}$ |
| $h$ in Js | $6.6\cdot 10^{-34}$ |
| $\varepsilon_0$ in As/(Vm) | $8.85\cdot 10^{-12}$ |
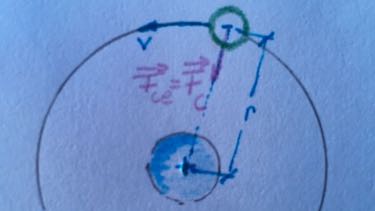
- Calculate the radius of the first three orbits.
- Calculate the velocity of the electrons on the first three orbits.
- Calculate the kinetic and potential energy of the first three orbits: ground state, first, second and third excited state.
- Calculate the ratio between Coulomb force and gravitational force of an electron on the first orbit.
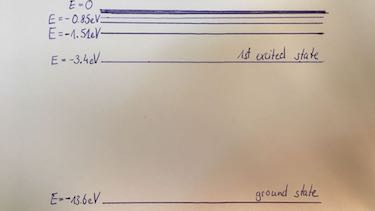
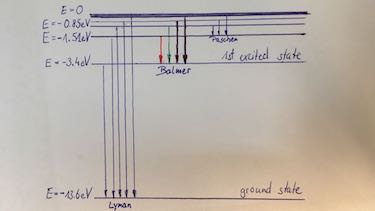
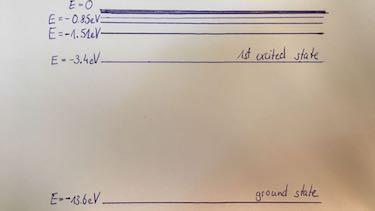
- Draw the energy levels of the Hydrogen atom.
- radius $r$ of orbit $n$:
$n$ 1 2 3 $r$ in 10-10 m $0.529$ $2.117$ $4.763$ - velocity $v$ of electrons on orbit $n$:
$n$ 1 2 3 $v$ in 106 m/s $2.188$ $1.094$ $0.729$ - energy levels:
orbit number $n$ 1 2 3 $E$ in eV $-13.6$ $-3.4$ $-1.5$
- Coulomb force: $F_C=$
gravitational force: $F_G=$
ratio: $\frac{F_C}{F_G}=\frac{}{}$ - energy levels of Hydrogen:
Question 3 ionisation energy
The ionisation energy of Aluminium is 5.99 eV. Assume the energy level for 1st excited state is 1.99 eV and for 2nd excited state is 1.49 eV.
- Draw a energy level diagram.
- Calclulate all possible energies of transition.
- Decide which transition is in the visible spectrum.

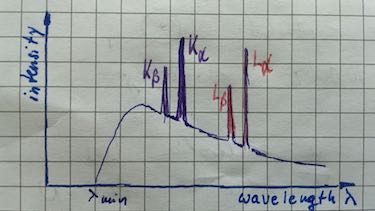
Question 4 X-ray spectrum
The characteristic X-ray spectrum for different elements is examined.
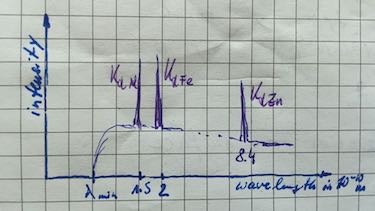
| element | Al | Fe | Zn |
| $\lambda_{K_\alpha}$ in 10-10m | $8.36$ | $1.95$ | $1.45$ |
- Calculate the corresponding energy for the first excited state.
- Draw a wavelength-intensity spectrum of a sample with these three metals.
-
element Al Fe Zn $\lambda_{K_\alpha}$ in 10-10m $8.36$ $1.95$ $1.45$ $E$ in keV $1.48$ $6.36$ $8.55$ -
Terms and phrases
| Niels Bohr | Danish physicist who described the atomic model with electrons circulating around the nucleus on certain energy levels. |
| nucleus | The central area of an atom, consisting of protons and neutrons. |
| electron transition | If atoms absorb enough energy, electrons can change their orbit. |
| ground state | lowest energy level in an atom |
| excited state | electrons on higher energy levels than ground state |
| ionisation energy | energy for an electron to jump from the ground state to the top of potential wall. |
| energy level diagram | a diagram which shows all possible states and the possible transitions |
| Balmer series | Emission spectrum from Hydrogen which show only the transition to the 1st excited states. 4 lines are visible. |
| dark lines in emission spectrum | occurs if the emitted spectrum is partly absorbed by the surrounding gas |
| characteristic X-ray spectrum | Transition to the ground state (K-orbit) is named $K_\alpha,\: K_\beta,\: K_\gamma$ radiation. Transition to the first excited state (L-orbit) is named $L_\alpha,\: L_\beta,\: L_\gamma$ radiation. |
© mylime.info