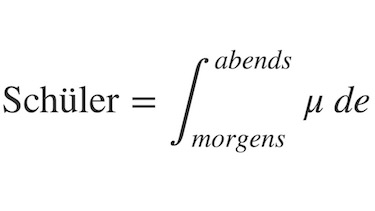Integral, Obersummen und Fläche - von der Rate zum Bestand
Aufgabe 1 Integral und Fläche
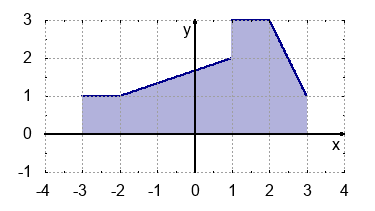
Die Funktionen der abgebildeten Schaubilder sind jeweils stückweise über ein Intervall definiert. Bestimme die Funktionsterme des Integrals und den entsprechenden Flächeninhalt im angegeben Intervall:
$$\int_{-3}^{3} f(x) \: dx $$- $= \int_{-3}^{-1} 1 \: dx + \int_{-1}^{1} x+2 \: dx $ $+ \int_{1}^{2} 3 \: dx + \int_{2}^{3} (-x+5) \: dx $ $= 2 + 4 +3 +2,5 = 11,5$
- $= \int_{-3}^{-1} 2 \: dx + \int_{-1}^{1} -x+1 \: dx $ $+ \int_{1}^{2} x \: dx + \int_{2}^{3} 1 \: dx $ $= 4 + 2 + 1,5 + 1 = 8,5$
- $= \int_{-3}^{-2} 1 \:\hspace{-0.5mm} dx + \int_{-2}^{1} \frac{1}{3}x+\frac{5}{3} \:\hspace{-0.5mm} dx $ $+ \int_{1}^{2} 3 \:\hspace{-0.5mm} dx + \int_{2}^{3} (-2x+7) \:\hspace{-0.5mm} dx $ $= 1 + 4,5 +3 + 2 = 10,5$
- $= \int_{-3}^{3} f(x) \: dx = 9$
Aufgabe 2 Wasserverbrauch in der Halbzeitpause
Das Wasserversorgungsunternehmen beobachtet in der Halbzeitpause einen deutlichen Anstieg des Wasserverbrauchs. Bestimme durch Approximation die verbrauchte Wassermenge während den 15 Minuten.

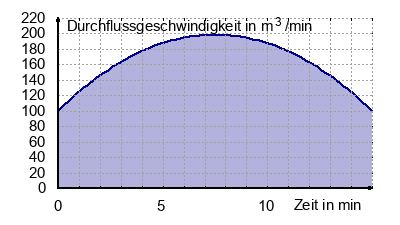
Die verbrauchte Wassermenge beträgt etwa 2300 m3.
Aufgabe 3 Der Fahrtenschreiber
Ein Fahrtenschreiber hat die Geschwindigkeit eine LKWs mitgezeichnet.
- Berechne wie viele Kilometer der LKW zwischen 08.00 Uhr und 08.30 Uhr zurückgelegt hat.
- Ermittle näherungsweise wieviele Kilometer der LKW zwischen 08.30 Uhr und 09.00 Uhr zurückgelegt hat.
- Wie viele Kilometer hat der LKW im gesamten Zeitraum zurückgelegt?
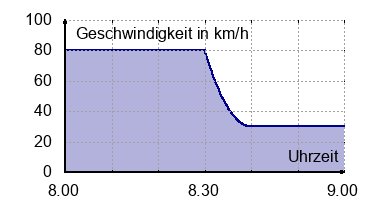
- zwischen 08.00 Uhr und 08.30 Uhr:
$s=\int_{0}^{0.5} 80 \: dt$ $= 80\: km/h \cdot 0.5\: h=40\: km$ - zwischen 08.30 Uhr und 09.00 Uhr:
$s=\int_{0.5}^{1} v(t) \: dt \approx 18\: km$ - zwischen 08.00 Uhr und 09.00 Uhr:
$s=\int_{0}^{1} v(t) \: dt \approx 58\: km$
Aufgabe 4 symmetrische Flächen
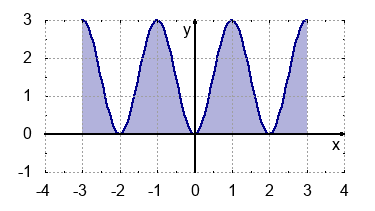
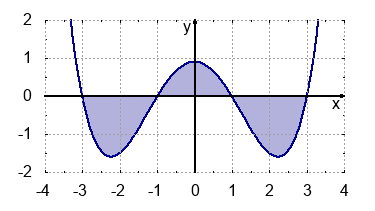
Die Schaubilder der abgebildeten sind symmetrisch. Notiere jeweils das dargestellte Integral und beurteile ob der Flächeninhalt positiv, negativ oder gleich 0 ist.
- positive Fläche: $$\int_{-2.5}^{2.5}f(x) \: dx=2,22$$
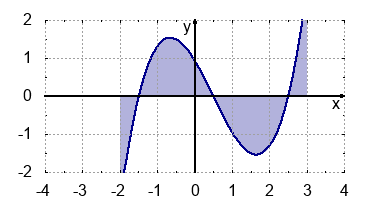
- negative Fläche: $$\int_{-3}^{3}f(x) \: dx=-2.88$$
- Fläche gleich 0: $$\int_{-2}^{3}f(x) \: dx=0$$
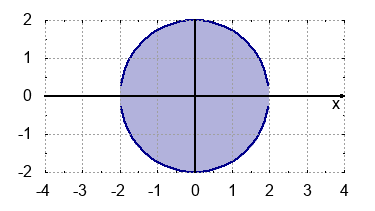
- zwei Halbkreise mit der Fläche $+2\pi$ und $-2\pi$: $$\int_{-2}^{2}\hspace{-2mm} f(x) \: dx+\int_{-2}^{2}\hspace{-2mm}g(x) \: dx=0$$
Aufgabe 5 Obersummen
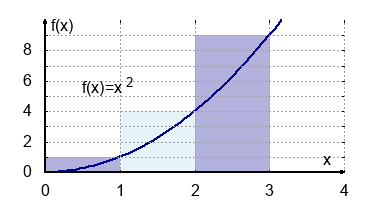
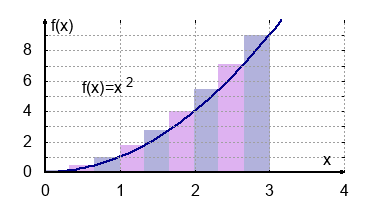
Berechne für die folgenden Funktionsterme die Flächen mit Hilfe der Obersummen für $n_1=5$, $n_2=10$, $n_3=100$ und $n \to \infty$ Abschnitte im Intervall von 0 bis $x_0=2$.
- $A=\int_{0}^{2} x \: dx$
- $A=\int_{0}^{2} x^2 \: dx$
- $A=\int_{0}^{2} x^3 \: dx$
- $A=\int_{0}^{2} x^2+2x \: dx$
- Berechne jeweils allgemein für das Intervall von 0 bis $x_0$ den Grenzwert für n → ∞
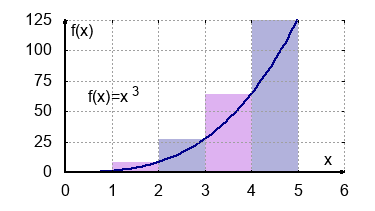
$A=\left(\frac{x_0}{n}\right)^2\: \frac{n(n+1)}{2}$
$n$ 5 10 100 n → ∞ $A$ 2,4 2,2 2,02 2 $A=\left(\frac{x_0}{n}\right)^3 \: \frac{n(n+1)(2n+1)}{6}$
$n$ 5 10 100 n → ∞ $A$ 3,52 3,1 2,71 8/3 $A=\left(\frac{x_0}{n}\right)^4 \:\frac{n^2(n+1)^2}{4}$
$n$ 5 10 100 n → ∞ $A$ 5,76 4,84 4,08 4 $A=\left(\frac{x_0}{n}\right)^3 \: \frac{n(n+1)(2n+1)}{6} $$+ 2\left(\frac{x_0}{n}\right)^2 \:\frac{n(n+1)}{2} $
$n$ 5 10 100 n → ∞ $A$ 8,3 7,5 6,75 20/3