Skischanze

Quadratische Funktionen

Die allermeisten Flugbahnen lassen sich durch eine quadratische Funktion berechnen. Sei es beim Springen, Volley- oder Fußballspielen, aber auch viele Brücken sind so konstruiert. Die quadratische Funktion und ihre Eigenschaften wird an Beispielen erklärt.

1 Ein umstrittener Aufschlag

Olympia 2012:
Ein umstrittenen Aufschlag beim Beachvolleyballfinale sorgt für Aufregung. Der Aufschlag von Olympiasieger Julius Brink und Jonas Rettermann soll angeblich im Aus gewesen sein. Computeranalysen ergaben im Bereich $-8 \leq x \leq 8$ eine Funktion f mit

$$f(x)=-\frac{1}{50}x^2-\frac{4}{25}x+\frac{64}{25}$$

War der Ball tatsächlich im Aus?

|enaktiv

2 Schnittpunkte mit der x-Achse
Volleyballaufschlag als Parabel

Die Funktion $f(x)=ax^2+bx+c$ heißt quadratische Funktion. Das Schaubild der Funktion heißt Parabel.

Schnittpunkte mit der x-Achse:
$\begin{align} &\Leftrightarrow f(x)=0 \\ &\Leftrightarrow -\frac{1}{50}x^2-\frac{4}{25}x+\frac{64}{25} = 0\\ &\Leftrightarrow x^2+8x-128 = 0\\ &\Leftrightarrow x_1=8 \lor x_2 = -16 \Rightarrow N(8|0) \end{align}$

Der Ball geht auf die Linie. Aber wie knapp geht der Ball über das Netz?

3 Schnittpunkt mit der y-Achse
Volleyballaufschlag als Parabel

Die Schnittpunkte mit der x-Achse heißen Nullstellen, der Schnittpunkt mit der y-Achse berechnet man durch Einsetzen von $x=0$ in den Funktionsterm.
$f(0)=-\frac{1}{50}\cdot 0 -\frac{4}{25} \cdot 0 +\frac{64}{25} = \frac{64}{25}$

$\Rightarrow S_y(0|2,56) \Rightarrow$ Der Ball geht 8 cm übers Netz.

Merke: Der Schnittpunkt mit der y-Achse der quadratischen Funktion mit $f(x)=ax^2+bx+c$ ist an der Stelle $y=c$.

4 Scheitelpunkt der Parabel

Der Extrempunkt (höchste oder tiefste Punkt) der Parabel wird als Scheitelpunkt $SP\left( x_{SP}|f(x_{SP})\right)$ bezeichnet. Er berechnet sich zu:

$$x_{SP}=-\frac{b}{2a}=-4$$

Alternativ erhalten wir ihn über Symmetrieüber­legungen: der Scheitelpunkt liegt zwischen den Nullstellen $x_{N1}$ und $x_{N1}$. $x_{SP}=\frac{x_{N1}+x_{N2}}{2}=\frac{8+(-16)}{2}=-4$

Den zugehörigen y-Wert erhalten wir durch einsetzen:
$f(-4)=2,88 \Rightarrow SP(-4|2,88)$
Der Ball wird max. 40 cm über Netzhöhe gespielt.

5 Die Brücke über den Sambesi

Genau unterhalb der Viktoriafälle wurde eine Eisenbahnbrücke errichtet, die heute zum Bungeejumping verwendet wird. Der parabelförmige Bogen hat eine Spannweite von 160 m und eine Höhe von 25 m

Hierfür wollen wir den Bogen konstruieren. Bei der Konstruktion kann man drei Dinge bestimmen: Die Form der Parabel, die Verschiebung in y-Richtung und die Verschiebung in x-Richtung.

6 Form und Lage einer Parabel
Brückenkonstruktion über den Sambesi

Der Parameter $a$ bestimmt die Form der Parabel: $f(x)=ax^2$
Dabei gilt: $a>0 \Leftrightarrow$ nach oben geöffnet, $a<0\Leftrightarrow$ nach unten geöffnet, $a=1 \Leftrightarrow$ Normalparabel.

Verschiebung in y-Richtung: $f(x)=ax^2+c$
Dabei gilt: $c>0 \Leftrightarrow$ nach oben, $c<0\Leftrightarrow$ nach unten.

Verschiebung in x-Richtung: $f(x)=a(x-d)^2$
Dabei gilt: $d>0 \Leftrightarrow$ nach rechts, $d<0\Leftrightarrow$ nach links.

Geht man von einer Ursprungsparabel aus, hat diese einen Punkt an der Stelle P(80|-25). Setzt man diesen in $f(x)=ax^2$ ein, erhält man $a=-1/256$.

7 Die Scheitelpunktform

Die Scheitelpunktform der quadratische Funktion lautet:

$$f(x)=a(x-x_{SP})^2+y_{SP}$$

Berechnet man durch Einsetzen eines Punktes in $f(x)=ax^2$ den Formfaktor $a$ und hat den Scheitelpunkt gegeben erhält man sofort den Funktionsterm. In unserem Beispiel mit $a=-1/256$ und dem Scheitelpunkt $SP(80|25)$:

$$f(x)=-\frac{1}{256}(x-80)^2+25$$

In dem Video wird der Weg von der Normalform zur Scheitelpunktform erklärt.

8 Gegenseitige Lage zweier Parabeln
zwei sich schneidende Parabeln

Gegeben sind $f(x)=-0,25x^2+1$ und $g(x)=0,25x^2-1$.

Bedingung für Schnittpunkte: $f(x)=g(x)$
$\begin{align} &\Leftrightarrow -0,25x^2+1=0,25x^2-1 \\ &\Leftrightarrow 0,5x^2 = 2\\ &\Leftrightarrow x_1=-2 \lor x_2 = 2\\ \end{align}$

Einsetzen in $f(x)$ liefert den zugehörigen y-Wert. Hat die quadratische Gleichung nur eine Lösung (Verschieben um 2 nach rechts) gibt es einen Berührpunkt und hat sie keine Lösung (Verschieben um 1 nach unten) berühren sich die Parabeln nicht.



Aufgabe 1 Schaubilder der quadratischen Funktion

Erstelle eine Wertetabelle und zeichne die Schaubilder folgender quadratischer Funktionen.

  1. $f(x)=x^2$
  2. $f(x)=2x^2+1$
  3. $f(x)=(x-1)^2$
  4. $f(x)=-(x+2)^2+3$
  1. $f(x)=(x-3)^2+1$
  2. $f(x)=-(x-3)^2+1$
  3. $f(x)=0.5(x-1)^2$
  4. $f(x)=-0.25(x+2)^2+3$
  1. Die ersten 4 Schaubilder:
    Schaubilder quadratischer Funktionen

  1. Die letzten 4 Schaubilder:
    Schaubilder quadratischer Funktionen


Aufgabe 2 Schnittpunkte mit den Achsen

Bestimme die Schnittpunkte der Parabeln mit den Achsen.

  1. $f(x)=-0,5x^2+2x$
  2. $f(x)=\frac{1}{8}(4x^2-4x+1)$
  3. $f(x)=4x^2+4x+2$
  1. $f(x)=-(x-2)(x-3)$
  2. $f(x)=-3(x-2)^2+3$
  1. $N_{x1}(-4|0)$, $N_{x1}(0|0)$, $N_y(0|0)$
  2. $N_x(0,5|0)$, $N_y(0|\frac{1}{8})$
  3. kein Schnittpunkt mit der x-Achse, $N_y(0|2)$
  4. $N_{x1}(2|0)$, $N_{x2}(3|0)$, $N_y(0|-6)$
  5. $N_{x1}(1|0)$, $N_{x2}(3|0)$, $N_y(0|-9)$

Teste deinen Lernerfolg ...

Wie bestimmt man die Nullstellen der quadratischen Funktion?

  1. $f(x)=0$ lösen
  2. $f(0)$ berechnen
  3. $f(0)=x$ lösen


Wie viele Nullstellen hat eine quadratischen Funktion?

  1. 1,2 oder 3
  2. 0,1 oder 2
  3. immer 2

Wie berechnet man den Scheitelpunkt der Parabel?

  1. $x_{SP}=-\frac{b}{2a}$
  2. $x_{SP}=-\frac{b}{2b}$
  3. $x_{SP}=-\frac{b}{2}\pm \sqrt{a/2-b}$


Um wieviel ist die Parabel mit $f(x)=(x-3)^2$ verschoben?

  1. um 3 nach links
  2. um 3 nach rechts
  3. um 3 nach unten

Aufgabe 3 Nullstellen und Scheitelpunkt der Parabel

Bestimme die Schnittpunkte mit den Achsen, den Scheitelpunkt und zeichne die Parabel. Verwende, wenn sinnvoll, eine alternative Berechnungsmethode.

  1. $f(x)=3x^2-6x+2$
  2. $f(x)=x^2-1$
  3. $f(x)=\frac{1}{2}(x-1)(x-4)$
  1. $f(x)=0,5(x-4)^2-2$
  2. $f(x)=-x(x+3)$

  1. 1. Schnittpunkte mit den Achsen:
    $N_{x1}(0.42|0)$, $N_{x1}(1,58|0)$, $N_y(0|2)$

    2. Scheitelpunkt: $SP(1|-1)$

    3. Schaubild:

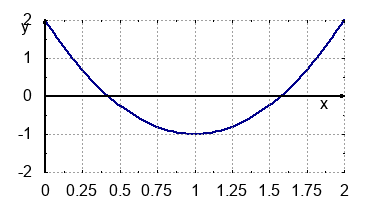
    Parabel

  2. 1. Schnittpunkte mit den Achsen:
    $N_{x1}(-1|0)$, $N_{x1}(1|0)$, $N_y(0|-1)$

    2. Scheitelpunkt: $SP(0|-1)$

    3. Schaubild:

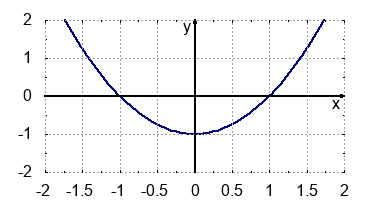
    Parabel

  3. 1. Schnittpunkte mit den Achsen:
    $N_{x1}(1|0)$, $N_{x1}(4|0)$, $N_y(0|2)$

    2. Scheitelpunkt: $SP(2,5|-9/8)$

    3. Schaubild:

    Parabel

  1. 1. Schnittpunkte mit den Achsen:
    $N_{x1}(2|0)$, $N_{x1}(6|0)$, $N_y(0|6)$

    2. Scheitelpunkt: $SP(4|-2)$

    3. Schaubild:

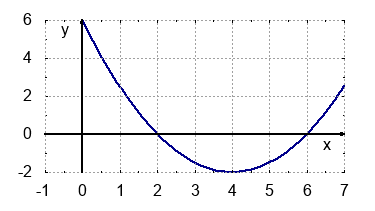
    Parabel

  2. 1. Schnittpunkte mit den Achsen:
    $N_{x1}(-3|0)$, $N_{x1}(0|0)$, $N_y(0|0)$

    2. Scheitelpunkt: $SP(-1,5|2,25)$

    3. Schaubild:

    Parabel

Entspann dich erst mal ...

Der Dorfuchs:

Ein Song über quadratische Funktionen, Parabeln und vor allem die Extremstelle bei $-b/(2a)$

Aufgabe 4 Hängebrücke

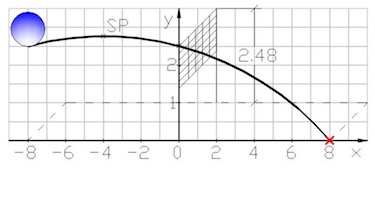
Das Tragseil einer Hängebrücke hat die Funktion:

$$f(x)=\frac{1}{5}x^2-\frac{7}{5}x+2$$
Hängebrücke

  1. Berechne die Höhe auf welcher das Seil über dem Fluß fixiert wurde.
  2. Prüfe, ob das Seil im Wasser hängt und falls ja gib die Punkte an.
  3. Berechne den tiefsten Punkt des Seiles und entscheide um wie viel man den Aufhängepunkt erhöhen müsste.
  4. Zeichne das Schaubild des Drahtseils.
  5. Gib den Wertebereich der Funktion für das Drahtseil an.
  1. y-Achsenabschnitt:
    $f(0)=2 \Rightarrow$ Ny(0|2)
    Antwort: Das Drahtseil ist zwei Meter über dem Boden fixiert.
  2. Nullstellen:
    $f(x)=0 \Leftrightarrow x_1=2 \text{und} x_2=5$
    N1(2|0), N2(5|0)
    Antwort: Das Drahtseil taucht an der Stelle $x=2$ ins Wasser ein und an der Stelle $x=5$ aus dem Wasser aus.
  3. Scheitelpunkt:
    $x_{SP}=-\frac{b}{2a}=3,5$
    $y_{SP}=f(3,5)=-0,45$
    SP(3,5|-0,45)
    Antwort: Der tiefste Punkt ist an der Stelle $x=3,5$ und dort hängt dast Seil 0,45 m im Wasser. Folgerichtig müsste man den Aufängepunkt um mehr als 0,45 m erhöhen, damit das Seil das Wasser nicht mehr berührt.
  4. Schaubild:
    Schaubild des Drahtseils

  5. Wertebereich
    $0\leq x \leq 7$

Aufgabe 5 Schnittpunkte

Autoren: D. Supper | DFU und binnendifferenziert

Wähle aus den folgenden Aufgaben eine aus, welche Dein Interesse am meisten weckt.

Die Fahrbahn des einen Autos wird mit dem Funktionsterm $f(x)=x^2-10x+28,5$ angegeben. Das zweite Auto fährt auf der Bahn $g(x)=-x^2+10x-19,5$.

  1. Begründe wie die Fahrbahnen verlaufen, damit die Autos zusammenstoßen können.
  2. Berechne die beiden Kreuzungspunkte der Fahrbahnen.
  3. Berechne die horizontale Entfernung der beiden Kreuzungspunkte.
  4. Berechne die größte vertikale Entfernung der beiden Autos zwischen den Kreuzungspunkten.
  5. Verschiebe die Fahrbahn des ersten Autos so, dass die beiden Fahrbahnen sich nur berühren.
2 Autos

Seeadler und Fisch

Die Flugbahn des Seeadlers wird mit dem Funktionsterm $f(x)=0,5x^2-20x+200$ angegeben. Der Fisch schwimmt auf der Geraden $g(x)=-0.1$.

  1. Begründe wie der Seeadler fliegen muss, damit er den Fisch greifen kann.
  2. Berechne den Ort, an dem der Fisch gegriffen werden kann.
  3. Berechne die Höhe des Seeadlers an der Stelle $x=0$.
  4. Berechne die kürzeste Entfernung zwischen Flugbahn des Seeadlers und der Fischgeraden.
  5. Begründe wieso eine parabelförmige Flugbahn für den Seeadler ideal ist.

Die Flugbahn eines Fußballs wird mit dem Funktionsterm $f(x)=-0,25x^2+5x$ angegeben. Der Vogel fliegt entlang der Geraden $g(x)=-0.1x+10$.

  1. Begründe wieso der Vogel vom Ball getroffen werden kann und berechne die Schnittpunkte.
  2. Berechne den Abstand der beiden x-Werte (horizontaler Abstand) der Schnittpunkte.
  3. Begründe wie die Flugbahn des Vogels verlaufen müsste, damit er den Ball nur berührt.
  4. Bestimme den x-Wert an dem der Vogel eine Höhe von 10  hat.
  5. Verschiebe die Flugbahn des Vogels in y-Richtung, so dass er dem Ball nicht in die Quere kommt. Gib den neuen Funktionsterm an.
Fußball und Vogel

Die 2 Autos:

  1. Die Autos können zusammenstoßen, wenn die beiden Fahrbahnen sich kreuzen oder berühren.
  2. Kreuzungspunkte: S1(4|4,5), S2(6|4,5)
  3. Die horizontale Entfernung der beiden Kreuzungspunkte beträgt 2 m.
  4. Die größte vertikale Entfernung der beiden Autos zwischen den Kreuzungspunkten beträgt 2 m.
  5. Verschobene Fahrbahn mit Berührpunkt: $f(x)=x^2-10x+30,5$

Seeadler und Fisch

  1. Der Seeadler muß so fliegen, dass er in seinem tiefsten Punkt die Wasseroberfläche berührt.
  2. Scheitelpunkt: SP(20|0)
  3. Höhe des Seeadlers an der Stelle $x=0$: $f(0)=200$
  4. Die kürzeste Entfernung zwischen Flugbahn des Seeadlers und der Fischgeraden im Scheitelpunkt beträgt 0,1 m..
  5. Der Seeadler kann so aus großer Höhe durch den nahezu senkrechten Blick aufs Wasser den Fisch erkennen und fliegt im Scheitelpunkt flach über das Wasser ohne plötzliche Richtungsänderungen.

Vogel und Fußball

  1. Der Vogel kann vom Fußball getroffen werden, wenn er dessen Flugbahn kreuzt.
    Die Schnittpunkte ergeben sich aus der Bedingung $f(x)=g(x)$ zu: S1(2,2|9,78), S2(18,2|8,18)
  2. Die horizontale Entfernung der beiden Schnittpunkte beträgt 16 m
  3. Der Scheitelpunkt der Fußballflugbahn ist an der Stelle $x=10$. Die Flugbahn des Vogels müsste um etwa 16 m höher verlaufen, damit er den Ball nur berührt.
  4. x-Wert an dem der Vogel eine Höhe von 5  hat: x=0.
  5. Verschiebe die Flugbahn des Vogels um +17 in y-Richtung, kommt er dem Ball nicht in die Quere: $g(x)=-0.1x+27$

Aufgabe 6 quadratischer Anstieg

Bei konstanter Beschleunigung mit $a=10\:\frac{m}{s^2}$ steigt die Strecke $s(t)=0,5at^2$ quadratisch.

Zeit in s 0 1 2 5 10
Strecke in m 0 5
  1. Vervollständige die Tabelle.
  2. Trage die Werte in ein Zeit-Strecke-Diagramm.
  3. Bestimme die Funktionsgleichung, falls zu Beginn bereits eine Strecke von 5 m zurückgelegt wurde.
  4. Bestimme die Funktionsgleichung, falls der Start 2 s verspätet beginnt. Definiere den Definitionsbereich.
Porsche

  1. Tabelle:
    Zeit in s 0 1 2 5 10
    Strecke in m 0 5 20 125 500
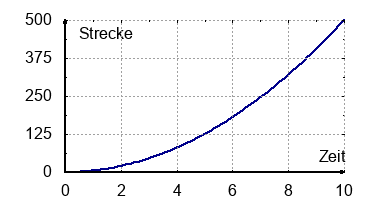
  2. Zeit-Strecke-Diagramm:
    Zeit-Strecke-Diagramm

  3. Funktionsgleichung: $s(t)=0,5at^2+5$
  4. Funktionsgleichung: $s(t)=0,5a(t-2)^2$, Definitionsbereich: $D: t \in \mathbb{R}^+$

Aufgabe 7 Der Fußballabstoß

Autoren: J. Blum, D. Supper | DFU und binnendifferenziert

Die Flugbahn eines Balles ist parabelförmig. Dies kann man bei einem Torabstoß, einem Golfschlag oder einer Kanonenkugel beobachten. Außeneinflüsse wie Wind und Anschneiden des Balles bleiben unberücksichtigt.

Im Folgenden soll die Flugbahn eines Balles auf dem Sportplatz analysiert werden. Vom Punkt O(0|0) wird der Ball abgeschlagen. Auf der x-Achse wird die Flugweite des Balles, auf der y-Achse die Flughöhe abgetragen.

Fußballstadion
  1. Beschreibe die allgemeine Bahngleichung unter Berücksichtigung des Abschlagpunktes.
    Parabel der Flugbahn

    Begründe, wieso in der allgemeinen Bahngleichung $f(x)=ax^2+bx+c$, der Parameter $a$ negativ ist und $c=0$ ist.

  2. Nach 30 m horizontaler Weite kommt der Ball wieder auf den Boden. Nach 6 m hat er eine Höhe von 7,20 m über dem Boden. Bestimme den Funktionsterm der Bahn.

    Bestimme zuerst zwei weitere Punkte des Graphen. Setze diese Punkte in den Funktionsterm ein und erstelle ein LGS mit 2 Lösungen. Durch lösen des LGS erhältst du die Parameter der Bahngleichung.

  3. Bestimme die maximale Höhe, die der Ball erreicht. Gib die zugehörige horizontale Weite an.

    Die maximale Höhe erreicht der Ball im Scheitelpunkt. Die horizontale Weite ist der x-Wert.

  4. Bestimme die horizontale Weite, bei welcher der Ball 8,80 m hoch ist. Gibt es vielleicht sogar mehr als einen?

Ein Vogel gleitet geradlinig über den Sportplatz auf der Suche nach Futter. Beim Startpunkt hat er eine Höhe von 12 m und bei 30 m horizontaler Weite ist er noch halb so hoch.

  1. Bestimme den Funktionsterm der Vogelflugbahn.

    Die Vogelflugbahn ist eine Gerade. Lies die Punkte aus dem Text und setzte sie in eine allgemeine Geradengleichung ein. Löse das lineare Gleichungssystem (LGS).

  2. Begründe weshalb der Vogel vom Ball getroffen werden kann und berechne die Schnittpunkte.
  3. Berechne den horizontalen Abstand zwischen den beiden Punkten.
  4. Berechne den Flächeninhalt des Vierecks, welches aus den Nullstellen und den beiden Schnittpunkten gebildet wird.
  1. Allgemeine Bahngleichung: $f(x)=ax2+bx$. Dabei ist der Parameter $a$ negativ, da die Parabel nach unten geöffnet ist und der Parameter $c=0$, da die Parabel die y-Achse an der Stelle $y=0$ schneidet.
  2. Bahngleichung: $f(x)=-0,05x^2+1,5x$
  3. Die maximale Höhe wird im Scheitelpunkt der Parabel erreicht: $SP(15|11,25)$. Der Ball erreicht nach 15 m horizontaler Weite seine maximale Höhe mit 11,25 m.
  4. Löse die Gleichung: $8,8=-0,05x^2+1,5x$
  5. Geradengleichung: $g(x)=-0,2x+12$
  6. Der Vogel kann vom Ball getroffen werden, wenn er die Flugbahn kreuzt. Dies tut er zweimal, denn es ergeben sich zwei Schnittpunkte mit der Geradengleichung: $A(10|10)$, B(24|7,2).
  7. Die Strecke zwischen den beiden Schnittpunkten beträgt 14 m.
  8. Das Trapez hat einen Flächeninhalt von 192 m2.

Aufgabe 7 proportionale und quadratische Zuordnungen

Gib Beispiele aus der Praxis an, in denen die Zuordnung proportional bzw. quadratisch ist.

Proportionale Zuordnungen:

  1. Die doppelte Menge an Hühnern, legen die doppelte Menge Eier. (Sylvia)
  2. Wenn man 2 Windräder besitzt, hat man doppelt so viel Energie und benötigt 2mal so viel Material. (Bennet)
  3. ...

Quadratische Zuordnungen:

  1. 1 Pferd zieht 100 kg, 2 Pferde ziehen 400 kg.
  2. Läuft ein Ventilator doppelt so schnell benötigt er die 4fache Menge an Energie.
  3. ...

Proportionale Zuordnungen:

  1. Die doppelte Menge an Hühnern, legen die doppelte Menge Eier. (Sylvia)
  2. Wenn man 2 Windräder besitzt, hat man doppelt so viel Energie und benötigt 2mal so viel Material. (Bennet)

Quadratische Zuordnungen:

  1. 1 Pferd zieht 100 kg, 2 Pferde ziehen 400 kg.
  2. Läuft ein Ventilator doppelt so schnell benötigt er die 4fache Menge an Energie.

Aufgabe 9 Wortschatzarbeit

Word cloud made with WordItOut

Erstelle eine "word cloud" mit allen wichtigen Fachbegriffen zum Thema quadratische Funktionen. Verwende hierfür den Word Cloud Generator:

Word cloud made with WordItOut

oder ein ähnliches Programm.

Kettenspiel: Einer beginnt und erklärt der Klasse den ersten Begriff. Dann wählt er einen neuen Begriff und gibt das Wort an den nächsten weiter.


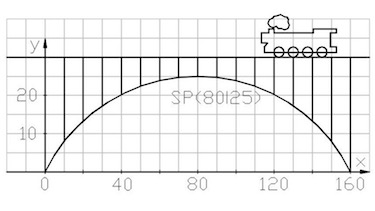
Aufgabe 10 Die Golden Gate Bridge - Konstruktion einer Hängebrücke

Autoren: D. Supper, J. Blum | DFU und binnendifferenziert

Die Golden Gate Bridge ist eine Hängebrücke und führt über eine Bucht bei San Francisco in den USA. Der mittlere Abschnitt hat eine Weite von etwa 1200 m. Das Stahlseil ist auf einer Höhe von 250 m über dem Meer befestigt und die Fahrbahn liegt 75 m über dem Meer.

Konstruktion der Golden Gate Bridge
  1. Bestimme den Formfaktor a des Funktionsterms $f(x)=ax^2$.

    Verschiebe die Parabel mit dem Scheitelpunkt SP auf den Ursprung. Bestimme nun wie weit du in x- und y-Richtung gehen musst, um auf den Aufhängepunkt zu kommen. Bestimme nun den Formfaktor, indem du diesen Punkt in die Gleichung $f(x)=ax^2$ einsetzt.

  2. Bestimme den exakten Funktionsterm $f(x)$ des Stahlseils im mittleren Brückenabschnitt.

    Setze den Formfaktor und Scheitelpunkt in die Scheitelpunktform $f(x)=a\left(x-x_{SP}\right)^2+y_{SP}$ein.

  3. Bestimme den Funktionsterm g(x) der Fahrbahn.
  4. Beschreibe zu welchem Punkt auf der Parabel f die Gerade g eine Tangente ist.

    Tangenten haben immer einen Berührpunkt.

  1. P(1200/2|250-75): $a=\frac{175}{600^2}=\frac{7}{14400}$
  2. Stahlseil: $f(x)=\frac{7}{14400}(x-600)^2+75$
  3. Fahrbahn: $g(x)=75$
  4. Die Gerade g ist eine Tangente im Scheitelpunkt SP(600|75) der Parabel f.

Wortliste und Satzbausteine



die quadratische Funktion, -en eine Funktion mit der Form: $f(x) = ax^2 + bx + c$, mit $a$ ungleich Null
der Funktionswert $f(x)$, -e der zugehörige Wert zu der Funktionsstelle $x$.
die Parabel, -n das Schaubild/der Graf der quadratischen Funktion, man erhält diesen indem man die einzelnen Wertepaare aus Funktionstelle und Funktionswert in einem Koordinatensystem aufträgt.
die Nullstelle, -n der Schnittpunkt mit der x-Achse
der Scheitelpunkt einer Parabel der höchste oder tiefste Punkt der Parabel
die Scheitel­punkt­form ein Funktionsterm $f(x)=a(x-x_{SP})^2+y_{SP}$ aus der man den Scheitelpunkt $SP(x_{SP}|y_{SP})$ der Parabel direkt ablesen kann.
der Schnittpunkt zweier Parabeln Gemeinsamer Punkt von Parabel 1 und Parabel 2
© mylime.info