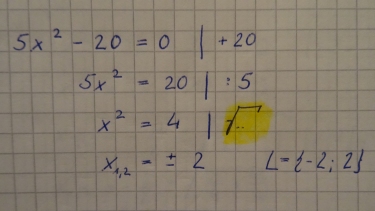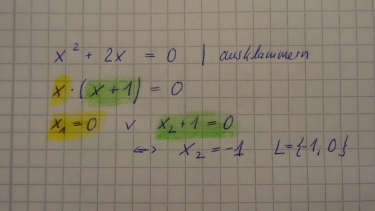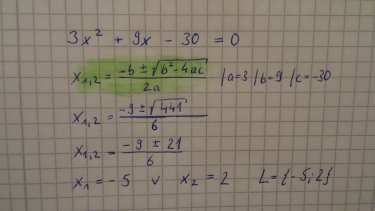Tomaten

Quadratische Glei­chungen

Hier wird erklärt, wie quadratische Gleichungen gelöst werden.

1 Rein quadratische Gleichungen
rein quadratische Gleichung

Quadratische Gleichungen haben allgemein die Form: $ax^2+bx+c=0$.

Ist $b=0$ spricht man von einer rein quadratischen Gleichungen.

Rein quadratische Gleichungen lassen sich einfach durch das Ziehen der Wurzel berechnen.

Ist der Wert unter der Wurzel positiv hat die quadratische Gleichung zwei Lösungen, ist der Wert Null, hat sie eine Lösung und ist der Wert negativ hat sie keine Lösung.

2 Satz vom Nullprodukt
quadratische Gleichung

Ist $c=0$ kann man ein $x$ ausklammern und erhält zwei Faktoren. Hier lassen sich die Lösungen dann ganz einfach mit dem sogenannten "Satz vom Nullprodukt" finden.

Ist ein Faktor in einem Produkt Null ist das gesamte Produkt Null.

Hinweis: Dieser Satz lässt sich auch anwenden, wenn die Gleichung in faktorisierter Form, wie $(x-3)(x-5)=0$, gegeben ist. In diesem Fall ist $x_1=3$ und $x_2=5$.

3 Quadratische Ergänzung
quadratische Gleichung

Allgemein kann eine quadratische Glei­chung mit der sogenannten quadra­ti­schen Ergänzung gelöst werden. Hierzu wird der linke Teil der Gleichung zu einer binomischen Formel ergänzt. Zuerst teilt man die Gleichung durch $a$, so dass der Faktor vor dem $x^2$ eins wird. Nun addiert man $(b/2)^2$ und schon hat man eine leicht lösbare binomische Formel.

Mit etwas Übung ist dieses Verfahren sehr schnell und schult unsere mathematischen Fähigkeiten da es die binomischen Formeln mit den quadratischen Gleichungen verknüpft.

4 pq-Formel
pq-Formel

Verallgemeinert man das Verfahren der quadratischen Ergänzung mit Variablen, dann erhält man die sogenannte pq-Formel. Auch hier teilt man die Gleichung durch $a$, so dass der Faktor vor dem $x^2$ eins wird. Nun lautet die allgemeine quadratische Gleichung: $x^2+px+q=0$.

Lösung mit der pq-Formel:

$$x_{1,2}=-\frac{p}{2}\pm\sqrt{\left(\frac{p}{2}\right)^2-q}$$

5 abc-Formel
abc-Formel

Verallgemeinert man das Verfahren der quadratischen Ergänzung mit Variablen, ohne vorher durch $a$ zu teilen, dann erhält man die sogenannte abc-Formel. Mit der allgemeinen quadratischen Gleichung: $ax^2+bx+c=0$ erhält man als Lösung:

$$x_{1,2}=-\frac{-b \pm\sqrt{b^2-4ac}}{2a}$$

Man beachte: Eine quadratische Gleichung kann zwei, eine oder keine Lösung haben. Dies hängt immer vom Wert unter der Wurzel ab.



Aufgabe 1 rein quadratische Gleichungen

Löse die Gleichungen.

  1. $5x^2=125$

  2. $3x^2=27$

  3. $-8x^2+40=8$

  4. $x^2=1,21$

  1. $\frac{x^2}{4}=25$

  2. $\frac{3x^2}{27}=1$

  3. $(x-2)^2=9$

  4. $9x^2-24x+16=0$

  1. $x=\pm 5$

  2. $x=\pm 3$

  3. $x=\pm 2$

  4. $x=\pm 1,1$

  5. $x=\pm 10$

  6. $x=\pm 3$

  7. $x=2\pm 3$

  8. $x=4/3$


Teste deinen Lernerfolg ...

Die Gleichung $6x^2+2x=0$ lässt sich lösen durch?



Die Gleichung $7x^2+2x=2x+4$ lässt sich lösen durch?



Mit welchem Term muss die Gleichung $x^2-10x=-16$ quadtratisch ergänzt werden, damit man sie lösen kann?

Aufgabe 2 Satz vom Nullprodukt

Löse die Gleichungen.

  1. $2x^2+4x=0$

  2. $x^2-2x+5=5$

  3. $x^2-5x+2=2-4x$

  4. $x^3-x^2=0$

  1. $x^2-16=0$

  1. $L={-2;0}$

  2. $L={0;2}$

  3. $L={0;1}$

  4. $L={0;1}$

  5. $L={-4;4}$


Aufgabe 3 quadratische Ergänzung

Löse die Gleichungen.

  1. $x^2-5x+6=0$

  2. $x^2+13x+30=0$

  3. $6x^2-6x-36=0$

  4. $2x^2-20x+20=-22$

  5. $7x^2+14x-1=20$

  1. $x^2+8x+15=0$

  2. $x^2+3x+1,25=5,25$

  3. $x^2-2x+3=11$

  4. $8+x^2+6x=0$

  1. $L={2;3}$

  2. $L={-10;-3}$

  3. $L={-2;3}$

  4. $L={3;7}$

  5. $L={-3;1}$

  6. $L={-5;-3}$

  7. $L={-4;1}$

  8. $L={-2;4}$

  9. $L={-4;-2}$


Entspann dich erst mal ...

Auflockerungsübung 1

Suche Wörte mit mindestens drei h/H.

Finde möglichst viele in zwei Minuten?

Auflockerungsübung 2

Du hast wieder zwei Minuten Zeit. Finde Städtenamen mit nur 4 Buchstaben wie bspw. Wien.

... und los geht's

Aufgabe 4 quadratische Ergänzung

Löse die Gleichungen.

  1. $10-x^2=3x$

  2. $x^2=125-20x$

  3. $28x=60-x^2$

  4. $5x^2+14+4x=6x^2+3x-6$

  5. $9-2x-2x^2=8x-3x^2-12$

  1. $3x(x+2)=16+2x^2$

  2. $(x-3)(x-1)-48=0$

  1. $L={-5;2}$

  2. $L={-25;5}$

  3. $L={-30;2}$

  4. $L={-4;5}$

  5. $L={3;7}$

  6. $L={-8;2}$

  7. $L={-5;9}$


Entspann dich erst mal ...

Der Dorfuchs:

Ein Song über die $pq$-Formel:
$$x=-\frac{p}{2}\pm \sqrt{\left(\frac{p}{2}\right)^2 - q}$$

Aufgabe 5 Wortschatzarbeit

Word cloud made with WordItOut

Erstelle eine "word cloud" mit allen wichtigen Fachbegriffen zu den quadratischen Gleichungen. Verwende hierfür den Word Cloud Generator:

Word cloud made with WordItOut

oder ein ähnliches Programm.

Kettenspiel: Einer beginnt und erklärt der Klasse den ersten Begriff. Dann wählt er einen neuen Begriff und gibt das Wort an den nächsten weiter.

rein quadratische Gleichung

Wortliste und Satzbausteine



die qua­dratische Gleichung, -en Eine quadratische Gleichung ist eine Gleichung mit einer quadratischen Variablen: $x^2+2x=3$. Sie kann zwei, eine oder keine Lösung haben.
das Verhält­nis, -se das Verhältnis von $x$ und $y$ ist: $\frac{x}{y}$
die quadtratische Ergänzung, -en durch Addition eines quadratischen Terms, wird die Gleichung so ergänzt, dass die Summe mit Hilfe der binomischen Formel in ein Produkt umgestellt werden kann. Dadurch können quadratische Gleichungen gelöst werden.
der goldene Schnitt, -e Der goldene Schnitt beschreibt ein Größen­verhältnis zwischen zwei Längen und deren Gesamtlänge. Dieses Verhältnis wird vom Mensch als harmonisch wahr­genommen. In der Natur kommt der goldene Schnitt sehr häufig vor.
die allgemeine Form der quadratischen Gleichung $ax^2+bx+c=0$ mit den Parametern $a$, $b$, $c$
die rein quadratische Gleichung eine quadratische Gleichung mit $b=0$: $ax^2+c=0$
der Satz vom Nullprodukt "Ist ein Faktor in einem Produkt gleich Null, ist das gesamt Produkt Null." Dieser Satz kommt zur Anwendung wenn $c=0$ ist, denn dann lässt sich die quadratische Gleichung durch Ausklammern einfach in ein Produkt umwandeln: $x^2+2x=0 \Leftrightarrow x(x+2)=0$
die $pq$-Formel Die quadratische Gleichung mit $x^2+px+q=0$ hat die Lösung: $x_{1,2}=-\frac{p}{2}\pm\sqrt{\left(\frac{p}{2}\right)^2-q}$. Die Anzahl der Lösungen hängt immer vom Wert unter der Wurzel ab.
die $abc$-Formel Die quadratische Gleichung mit $ax^2+bx+c=0$ hat die Lösung: $x_{1,2}=-\frac{-b \pm\sqrt{b^2-4ac}}{2a}$. Die Anzahl der Lösungen hängt immer vom Wert unter der Wurzel ab.
© mylime.info