zeitlicher Verlauf des Wechselstroms am Oszilloskop

Trigonometrische Funktionen

Mit trigonometrischen Funktionen beschreibt man sich periodisch wiederholende Vorgänge, wie das Schwingen eines Pendels, Wechselstrom oder den Verlauf von Wellen.

1 Die Sinusfunktion
Einheitskreis und Liniendiagramm der Sinusfunktion

Zeichne einen Kreis mit dem Radius 2 cm. Unterteile den Kreis in 30 ° Abständen. Zeichne ein rechtwinkliges Dreieck für 30 ° ein. Markiere die Gegenkathete $y$.

Zeichne für jeden Winkel die Höhe der Gegenkathete $y$ in das Liniendiagramm. Du erhältst das Schaubild der Sinus-Funktion.

$$y=r\cdot sin(\alpha )$$

|enaktiv

2 Die Cosinusfunktion
Einheitskreis und Liniendiagramm der Cosinusfunktion

Wenn du für jeden Winkel die Länge der Ankathete $y$ in das Diagramm einträgst, erhältst du das Schaubild der Cosinus-Funktion.

$$y=r \cdot cos(\alpha )$$

Tipp: Die Ankathete liegt am Winkel $\alpha$, die Gegenkathete gegenüber $\alpha$ und die Hypothenuse gegenüber des rechten Winkels.

Neben der Sinus- und Cosinusfunktion gibt es unter den trigonometrischen Funktionen noch viele weitere, wie bspw. die Tangensfunktion. Alle trigonometrischen Funktionen sind periodisch, d.h. sie wiederholen sich ab einem bestimmten Punkt.

3 Sinus, Cosinus und Tangens
auf dem Bauernhof

Auch wenn wir es für die trigonometrischen Funktionen nicht unbedingt benötigen hier nochmal die Merkhilfe auf dem Bauernhof:

Auf dem Bauernhof in den Berchtesgardener Alpen gibt es die GAGA-Hühnerhof AG, kurz GAGA-HHAG. Nun schau dir dies an:

sin cos tan cot
G A G A
H H A G
4 Verschiebung in y-Richtung
Schaubilder der in y-Richtung verschobenen Sinusfunktion

Die Sinusfunktion $f(x)=sin(x)+c$ wird durch den Faktor $c$ in y-Richtung verschoben.

$x$ 0 $\frac{1}{2}\pi$ $\pi$
$f(x)=sin(x)$ 0 1 0
$g(x)=sin(x)-1$ -1 0 -1
$h(x)=sin(x)+2$ 2 3 2
5 Streckung in y-Richtung
Schaubild der in y-Richtung gestreckten Sinusfunktion

Für die Streckung in y-Richtung gilt: $f(x)=a sin(x)$. Dabei bezeichnet man $a$ als Amplitude.

$$f(x)=sin(x)$$

$$g(x)=2sin(x)$$

Alternativ kann man auch strecken und verschieben:

$$h(x)=0,5sin(x)-1$$



Aufgabe 1

  1. Schreibe einen Funktionsterm für eine $\sin$-Funktion mit einer Amplitude von $3$.
  2. Schreibe den Funktionsterm für eine $\cos$-Funktion mit einem Offset von $+2$.
  3. Schreibe einen Funktionsterm für eine $\sin$-Funktion mit einer Amplitude von $2$ und einer Verschiebung um $+\pi$.
  1. $f(x)=3\cdot \sin x$
  2. $f(x)=\cos x+2$
  3. $f(x)=2\cdot \sin (x-\pi )$

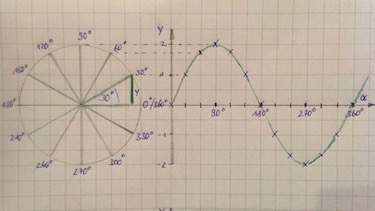
Aufgabe 2 Zuordnung von Schaubildern

Welche Beschreibung passt?

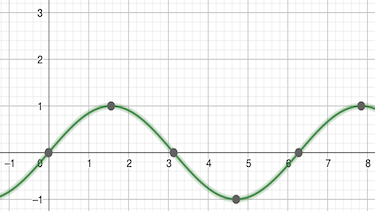
Schaubild trigonometrische Funktion

  1. Der Funktionsterm lautet ...

  2. Die Amplitude der allgemeinen trigonometrischen Funktion $f(x)=a\cdot \sin(x) + b$ ist ...

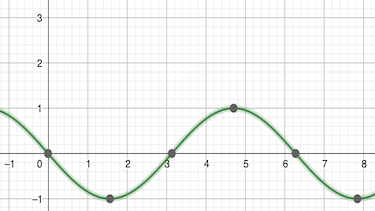
Schaubild trigonometrische Funktion

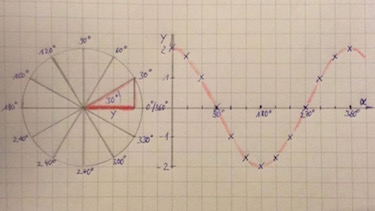
  1. Der Funktionsterm lautet ...

  2. Von der allg. trigonometrischen Funktion $f(x)=a \cdot \sin (x)+b$ beschreibt $b$ ...

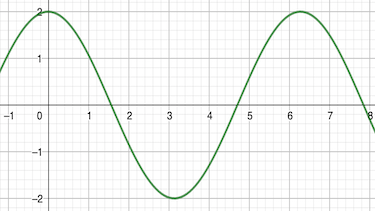
Schaubild trigonometrische Funktion

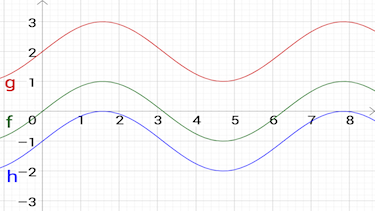
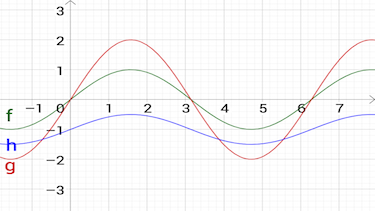
  1. Die Funktionsvorschrift lautet ...

  2. Die Anzahl an Nullstellen von triogonometrischen Funktionen ist ...



Aufgabe 3 Nullstellen

Gegeben ist die trigonometrische Funktion $f(x)=2\cdot sin(x-\pi)$

  1. Bestimme den Schnittpunkt mit der y-Achse.
  2. Bestimme die Nullstellen im Intervall $[0,2\pi]$.
  3. Bestimme die Maxima im Intervall $[0,2\pi]$.
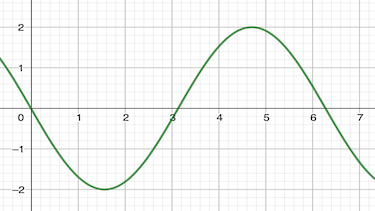
Schaubild Sinusfunktion

  1. Schnittpunkt y-Achse: Ny($0$|$0$)
  2. Schnittpunkte x-Achse: Nx1($0$|$0$), Nx2($\pi$|$0$), Nx3($2\pi$|$0$)
  3. Extrmpunkte: TP1($\pi/2$|$-2$), HP2($3/2\pi$|$2$)

Wortliste und Satzbausteine



die trigono­metrische Funktion, -en eine Funktion mit der Form: $f(x) = a\cdot \sin (x)$, $f(x) = a\cdot \cos (x)$mit $a$ oder $f(x) = a\cdot \tan(x)$, mit $a$ ungleich Null
der Funktions­wert $f(x)$, -e der zugehörige Wert zu der Funktionsstelle $x$.
periodisch in gleichen Abständen regelmäßig auftretend
© mylime.info