
Analytische Geometrie - Vektoren und Geraden
Aufgabe 1 Stadttor
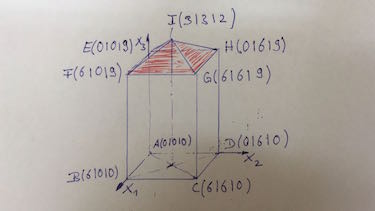
Der Turm des Stadttors hat eine Länge und Breite von 6 m und eine Höhe von 9 m. Das pyramidenförmige Dach hat eine zusätzliche Höhe von 2 m.
Bestimme alle Koordinaten der Eckpunkte und der Turmspitze.

Aufgabe 2 Richtungsvektoren

Gegeben sind die Eckpunkte der Schokoladentafel A(0|0|0), B(4|0|0), C(4|4|0) und D(0|4|0).
- Bestimme die Richtungsvektoren $\vec{AB}$, $\vec{AC}$ und $\vec{AD}$.
- Addiere die beiden Richtungsvektoren $\vec{AB}$ und $\vec{AD}$.
- Bestimme den Richtungsvektor $\vec{DB}$.
- Bestimme das 3fache des Richtungsvektors $\vec{AC}$ und die Koordinaten des Punktes.
- Richtungsvektoren:
$\vec{AB}=\left(\begin{array}{c} 4 \\ 0 \\ 0 \end{array}\right)$, $\vec{AC}=\left(\begin{array}{c} 4 \\ 4 \\ 0 \end{array}\right)$, $\vec{AD}=\left(\begin{array}{c} 0 \\ 4 \\ 0 \end{array}\right)$ - Addition von Vektoren: $\vec{AB}+\vec{AD}=\left(\begin{array}{c} 4 \\ 4 \\ 0 \end{array}\right)$
- Richtungsvektor:
$\vec{DB}=\left(\begin{array}{c} 4 \\ -4 \\ 0 \end{array}\right)$ - Parameter: $3\cdot \vec{AC}=\left(\begin{array}{c} 12 \\ 12 \\ 0 \end{array}\right)$
Punkt: P(12|12|0)
Aufgabe 3 Geraden
Gegeben sind die beiden Geraden g: $\vec{x}=\left(\begin{array}{c} 1 \\ 3 \\ -2 \end{array}\right)+s\left(\begin{array}{c} 4 \\ 9 \\ 3 \end{array}\right)$ und h: $\vec{x}=\left(\begin{array}{c} 5 \\ 12 \\ 1 \end{array}\right)+t\left(\begin{array}{c} 8 \\ 1 \\ 0 \end{array}\right)$.
- Benenne die beiden Ortsvektoren und die beiden Richtungsvektoren.
- Bestimme die Punkte, wenn man für die Parameter den Wert $s=t=2$ einsetzt.
- Bestimme den Schnittpunkt der beiden Geraden.

- Ortsverktoren: $\left(\begin{array}{c} 1 \\ 3 \\ -2 \end{array}\right)$, $\left(\begin{array}{c} 5 \\ 12 \\ 1 \end{array}\right)$
Richtungsvektoren: $\left(\begin{array}{c} 4 \\ 9 \\ 3 \end{array}\right)$, $\left(\begin{array}{c} 8 \\ 1 \\ 0 \end{array}\right)$ - A(9|21|4), B(21|14|1)
- Schnittpunkt S(5|12|1)
Wortliste und Satzbausteine
| der Vektor, -en | eine mathematische Größe mit einer Länge und Richtung |
| die Linearkombination, -en | z.B. Multiplikation einer Zahl mit einem Vektor: $r\cdot \vec{a}$ |
| der Orts- oder Stützvektor, -en | Der Ortsvektor zeigt vom Ursprung auf den Anfangspunkt einer Geraden |
| der Richtungsvektor, -en | gibt die Richtung von einem Punkt aus an |
| die Gerade, -n | eine Linie im Raum, welche durch einen Ortsvektor und dem Vielfachen eines Richtungsvektors beschrieben wird |
| der Punkt, -e | wird durch Koordinaten im Raum festgelegt |
© mylime.info



