1 Euro Münze

Exponentialfunktion

Mit Exponentialfunktionen berechnet man den Zinsverlauf, den radio­aktiven Zerfall von Atomen und viele weitere Vorgänge in der Natur. Exponential­funktionen und ihre Eigenschaften werden an praktischen Beispielen erklärt.

1 Eine Epidemie breitet sich aus
Schaubild einer Exponentialfunktion

Eine Virusepidemie breitet sich aus:
Am Tag 0 wird ein Patient verzeichnet, am Tag 1 zwei Patienten, am Tag 2 vier Patienten und so verdoppelt sich die Anzahl der Patienten jeden Tag.

Spielt den Vorgang im Klassenzimmer durch. Wie lange dauert es, bis alle Schüler erkrankt sind?

Ein solcher Verlauf wird mit der Exponentialfunktion $f(x)=2^x$ dargestellt. Erkranken durchschnittlich täglich die 1,5fache Menge an Personen haben wir $f(x)=1,5^x$ und so weiter.

|enaktiv

2 Die Exponential­funktion $f(x)=a^x$
Schaubild der Exponentialfunktion

Die Funktion $f(x)=a^x$ heißt Exponentialfunktion, da $x$ im Exponenten steht. Halbiert sich der Funktionswert täglich gilt $f(x)=0,5^x$, mit $g(x)=2^x$ verdoppelt er sich.

$x$ -1 0 1 2
$f(x)=0,5^x$ 2 1 0,5 1/4
$g(x)=2^x$ 0,5 1 2 4
$h(x)=3^x$ 1/3 1 3 9
3 Verschiebung in y-Richtung
Schaubilder der in y-Richtung verschobenen Exponentialfunktion

Die Exponentialfunktion $f(x)=a^x+b$ wird durch den Faktor $b$ in y-Richtung verschoben.

$x$ -1 0 1 2
$f(x)=2^x-2$ -1,5 -1 0 2
$g(x)=2^x$ 0,5 1 2 4
$h(x)=2^x+2$ 2,5 3 4 6
4 Verschiebung in x-Richtung
Schaubilder der in x-Richtung verschobenen Exponentialfunktion

Die Exponentialfunktion $f(x)=a^{x-d}$ wird durch den Faktor $d$ in x-Richtung verschoben.

$x$ -1 0 1 2
$f(x)=2^{x+2}$ 2 4 8 16
$g(x)=2^x$ 1/2 1 2 4
$h(x)=2^{x-2}$ 1/16 1/8 1/4 1/2
5 Spiegelung an der x- und y-Achse
Schaubild gespiegelter Exponentialfunktionen

Möchte man die Funktion $g(x)=2^x$ zur y-Achse spiegeln berechnet man:

$$h(x)=g(-x)=2^{-x}$$

Für die Spiegelung an der x-Achse gilt:

$$f(x)=-g(x)=-2^{x}$$

6 Stauchung und Streckung
Schaubilder der Exponentialfunktion

Mit dem Parameter $k$ der Funktion $f(x)=k\cdot a^x+b$, wird die Funktion gestaucht oder gestreckt. $b$ gibt die Lage der Asymptote an und $k+b$ den y-Achsenabschnitt.

$x$ -1 0 1 2
$f(x)=0,5\cdot 2^x$ 1/4 0,5 1 2
$g(x)=2^x$ 0,5 1 2 4
$h(x)=2\cdot 2^x+1$ 2 3 5 9
7 Der radioaktive Zerfall
radioaktiv

Radioaktives Jod besitzt eine Halbwertszeit von etwa 8 Tagen. Das bedeutet bspw. bei einer Anfangsdosis $k=10$ mg sind nach dieser Zeit nur noch die Hälfte vorhanden. Dieser Zerfall wird allgemein mit der Gleichung $f(x)=k\cdot a^x$ beschrieben, wobei $x$ die Zeit in Tagen angibt.

Zur Bestimmung des Parameters $a$ nutzen wir die angegebenen Werte und schreiben mit $5=10 \cdot a^8$. Lösen dieser Gleichung liefert $a=\sqrt[8]{0,5}=0,917$. Damit folgt der Funktionsterm für den radioaktiven Zerfall:

$$f(x)=10\cdot 0,917^x$$
8 Nullstellen
Schaubild der Exponentialfunktion

Gegeben sind $f(x)=2^x=e^{ln(2) \cdot x}$ und $g(x)=e^{ln(2) \cdot x} - 2$.

Während das Schaubild $f$ keine Nullstelle hat, erhalten wir die Nullstelle für $g$ durch lösen von $g(x)=0$:
$\begin{align} &\Leftrightarrow e^{ln(2)x}-2=0 \: |+2\\ &\Leftrightarrow e^{ln(2)x} = 2 \: |ln(..)\\ &\Leftrightarrow ln(2)x = ln(2) \: |:ln(2)\\ &\Leftrightarrow x=1 \\ \end{align}$

Berechnen von $g(0)=-1$ liefert den Schnittpunkt mit der y-Achse.



Aufgabe 1

  1. Schreibe einen Funktionsterm für ein dreifaches Wachstum pro Tag.
  2. Benenne eine Exponentialfunktion mit dem y-Achsenabschnitt von 3.
  3. Schreibe einen Funktionsterm für ein dreifaches Wachstum pro Tag und einem Startwert von 2.
  1. $f(x)=3^x$
  2. $f(x)=3^x+2$
  3. $f(x)=2 \cdot 3^x$

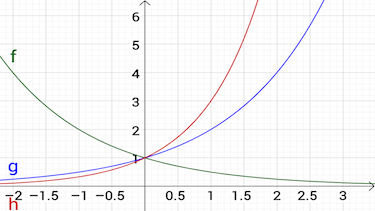
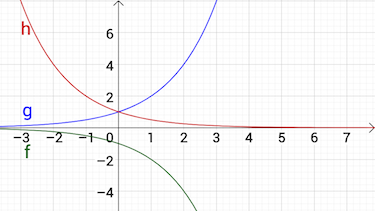
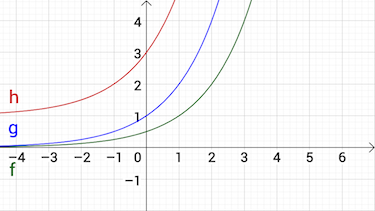
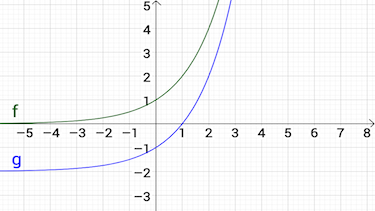
Aufgabe 2 Zuordnung von Schaubildern

Welche Beschreibung passt?

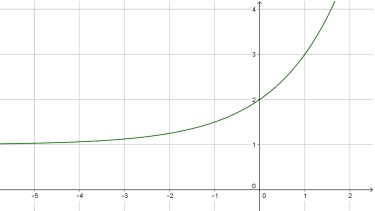
Exponentialfunktion

  1. Die Funktionsvorschrift lautet ...

  2. Der y-Achsenabschnit von der allgemeinen Exponentialfunktion $f(x)=k\cdot a^x + b$ ist ...

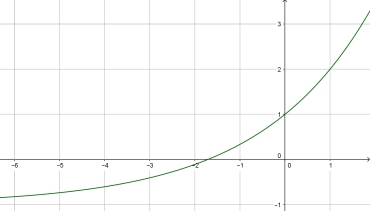
Schaubild Exponentialfunktion

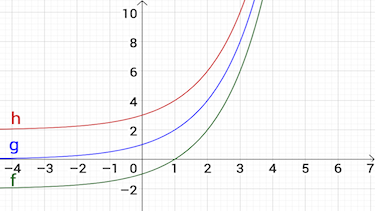
  1. Die Funktionsvorschrift lautet ...

  2. Von der allg. Exponentialfunktion $f(x)=k \cdot a^x+b$ beschreibt $b$ ...

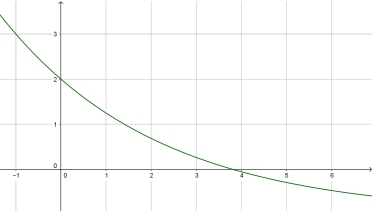
Schaubild Exponentialfunktion

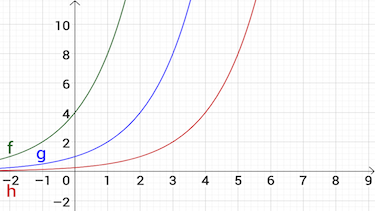
  1. Die Funktionsvorschrift lautet ...

  2. Die Nullstelle bestimmt man ...



Aufgabe 3 Infektionen

Bestimme den Funktionsterm $f(x)=k\cdot a^x$.

  1. Am Tag 0 haben 5 Kinder in der Schule Läuse, am Tag 1 sind es schon 8. (von Jasmin)
  2. Heute sind 367 Personen an einem Virus erkrankt. In drei Tagen sind es 2936 Personen. (von Hanna)
  3. 5 Kranke kamen 19.03.2019 ins Krankenhaus. Die Ärztin diagnostiziert Ampolesis. Am 20.03.2019 sind 40  Personen erkrankt. Die Ärztin vermutet eine tägliche Zunahme um den Faktor 5. Hat sie recht? (von Stefanie)
  4. Nachdem ein Heilmittel gegen ein Virus eingesetzt wurde, ging die Anzahl der Infektionen nach 2 Tagen von 27.000 auf 3.000 zurück. Berechne außerdem die Anzahl der Kranken nach 5 Tagen. (von Chris)
  5. Ein Organismus wird von 300 Viren befallen, die sich exponentiell vermehren. Pro Stunde wächst die Anzahl um 30 %.
    Nach wie viel Stunden sind es mehr als 1000 Viren?
icon biohazard

  1. mit $k=5$ und $8=5\cdot a^1$ folgt: $f(x)=5\cdot \left( \frac{8}{5} \right)^x$
  2. mit $k=367$ und $2936=367\cdot a^3$ folgt: $f(x)=367\cdot 2^x$
  3. mit $k=5$ und $40=5\cdot a^1$ folgt: $f(x)=5\cdot 8^x$. Die Krankheit breitet sich täglich mit dem Faktor 8 aus.
  4. mit $k=27000$ und $3000=27000\cdot a^2$ folgt: $f(x)=27000\cdot \left( \frac{1}{3} \right)^x$. $f(5)=27000\cdot \left( \frac{1}{3} \right)^5\approx 111$.
  5. mit $k=300$ und $300 \cdot 1,3 =300\cdot a^1$ folgt: $f(x)=300\cdot 1,3^x$.
    $f(x)\geq 1000$
    $300\cdot 1,3^x \geq 1000$
    $1,3^x \geq 10/3$
    $x\cdot \ln(1,3) \geq \ln(10/3)$
    $x \geq 4589...$

Aufgabe 4 Radioaktiver Zerfall

Die Nuklide (Spaltprodukte) Jod-131 und Caesium-137 welche in Atomreaktoren entstehen sind Gamma- und Betastrahler mit einer Halbwertszeit von 8 Tagen und 10950 Tagen. Während aus dem Jod-131 Caesiumkerne entstehen, entsteht aus den Caesiumkernen Bariumkerne. Die Anfangsmenge der Nuklide beträgt jeweils 100 mg.

radioaktiv

  1. Bestimme den Funktionsterm für Jod-131.
  2. Bestimme den Funktionsterm für Casium-137.
  3. Bestimme die Nuklidmenge nach 30 Tagen.
  4. Bestimme die Nuklidmenge nach 365 Tagen.
  5. Bestimme die Zeit nach der noch 25 % Jod-131 erhalten sind.
  6. Bestimme die Caesiummenge nach 30 Tagen unter der Berückschtigung, dass aus Jod-131 Caesiumkerne entstehen.
  1. Jod: $f(x)=100\cdot 0,5^{\frac{x}{8}} \approx 100\cdot 0,917^x $
  2. Cäsium: $f(x)=100\cdot 0,5^{\frac{x}{10950}} \approx 100\cdot 0,99994^x $
  3. $m_{J}=7,43\:$mg, $m_{Cs}=99,81\:$mg
  4. $m_{J}=1,84\cdot 10^{-12}\:$mg, $m_{Cs}=97,72\:$mg
  5. 11,46 Tage
  6. ...

Aufgabe 5 Zinswachstum

300 EUR werden mit jährlich 3 % Zinsen angelegt. Die Zinsen werden am Jahresende gutgeschrieben.

  1. Bestimme den Funktionsterm $f(x)=k\cdot a^x$.
  2. Wie hoch ist das Guthaben nach 4, 10 und 20 Jahren.
  3. Berechene, nach wie vielen Jahren das Guthaben auf über 1000 EUR angewachsen ist.
  4. Frau Kraus hat ihr Geld vor 10 Jahren zu 3 % angelegt und hat heute 1000 EUR Guthaben. Berechne ihr Anfangskapital.
EURO-Muenze

  1. $f(x)=300\cdot 1,03^x$
  2. $f(4)=337,65$ EUR
    $f(10)=403,17$ EUR
    $f(20)=541,83$ EUR
  3. $300\cdot 1,03^x\geq 1000$ $\Leftrightarrow$ $x\geq 40,73$ Jahre
  4. Ihr Anfangskapital betrug $K_0=1000/1,03^{10}\approx 744$ EUR.

Aufgabe 6 Ertrag

Ein Bauer hat 100 Haferkörner. Ein Haferkorn bringt pro Jahr einen 100fachen Ertrag.

Hafer

  1. Bestimme den Funktionsterm $f(x)=k\cdot a^x$.
  2. Wie hoch ist der Ertrag nach 10 und 20 Jahren.
  3. Berechene, nach wie vielen Jahren der Ertrag auf über 5.000.000 Haferkörner angewachsen ist.
  4. Berechene den Ertrag nach 10 Jahren, unter der Berücksichtigung, dass die eingesetzten Körner sterben.
  1. $f(x)=100\cdot 100^x$
  2. $f(10)=1\cdot 10^{22}$ Körner
    $f(20)=1\cdot 10^{42}$ Körner
  3. $2,35$ Jahre
  4. Das Sterben der Körner ist im Ertrag bereits berücksichtigt.

Wortliste und Satzbausteine



die Exponen­tial­funktion, -en eine Funktion mit der Form: $f(x) = a\cdot k^x$, mit $a$, $k$ ungleich Null
der Funktionswert $f(x)$, -e der zugehörige Wert zu der Funktionsstelle $x$.
die Asymptote, -n das Schaubild der Exponentialfunktion nähert sich einer Geraden, welche man Asymptote (Näherungsgerade) nennt.
die Epidemie, -n das Auftreten einer ansteckenden Krankheit
der Virus, Viren ein Krankheits­erreger
der radio­aktive Zerfall Umwandlungsprozess, bei dem Atomkerne Zerfallen
© mylime.info