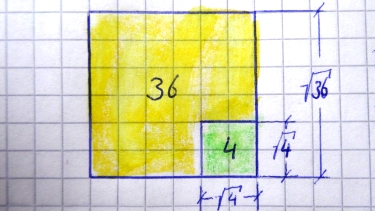
Quadratwurzel
12.11.2015Aufgabe 1
Berechne die Quadratwurzel
$\sqrt{4}$
$\sqrt{9}$
$\sqrt{16}$
$\sqrt{25}$
$\sqrt{36}$
$\sqrt{49}$
$\sqrt{64}$
$\sqrt{81}$
$\sqrt{100}$
$\sqrt{0,04}$
$\sqrt{0,4}$
$\sqrt{40}$
$\sqrt{400}$
$\sqrt{0,25}$
$\sqrt{0,025}$
$\sqrt{2500}$
$2$
$3$
$4$
$5$
$6$
$7$
$8$
$9$
$10$
$0,2$
$0,632...$
$6,32...$
$20$
$0,5$
$0,158...$
$50$
Aufgabe 2 Multiplikation und Division
Rechne ohne Taschenrechner.
$\sqrt{25 \cdot 16 \cdot 100}$
$\sqrt{4 \cdot 49 \cdot 9}$
$\frac{\sqrt{144}}{\sqrt{4}}$
$\frac{\sqrt{121}\cdot\sqrt{27}}{\sqrt{3}}$
$\sqrt{18} \cdot \sqrt{5} \cdot \sqrt{2} \cdot \sqrt{20}$
$\sqrt{40 000 \cdot 490 \cdot 90}$
$\sqrt{\frac{4000 \cdot 3 \cdot 12 }{10}}$
$\sqrt{0,5} \cdot \sqrt{160} \cdot \sqrt{0,5} \cdot \sqrt{40}$
- $\frac{\sqrt{108}}{\sqrt{12}}$
- $\sqrt{1,8} \cdot\sqrt{5}$
$200$
$42$
$6$
$33$
$60$
$42000$
$120$
$40$
- $\frac{\sqrt{324}}{\sqrt{36}}=3$
- $\sqrt{9}=3$
Aufgabe 3 Multiplikation und Division mit Variablen
Vereinfache.
$\sqrt{x} \cdot \sqrt{4x}$
$\sqrt{4a} \cdot \sqrt{9a}$
$\frac{\sqrt{144x^3}}{\sqrt{x}}$
$\frac{\sqrt{121n^2}\cdot\sqrt{27n}}{\sqrt{3n^2}}$
$\sqrt{n^4} \cdot \sqrt{8n^{-1}} \cdot \sqrt{4n^{-5}} \cdot \sqrt{2n^4}$
$\sqrt{x \cdot 490 \cdot 10x^3}$
$\sqrt{\frac{20b^3 \cdot 200b^2}{10b^3}}$
$2x$
$6a$
$12x$
$33\cdot \sqrt{n}$
$8n$
$70x^2$
$20b$
Aufgabe 4 Ausklammern
Vereinfache soweit als möglich.
$\sqrt{36} + \sqrt{64}$
$\sqrt{36+64}$
$\sqrt{100} - \sqrt{64}$
$\sqrt{100-64}$
$3\cdot \sqrt{n} + 4\cdot \sqrt{n}$
$(6\cdot\sqrt{6} - 4\cdot \sqrt{6}):\sqrt{6}$
$(6\cdot\sqrt{2} - 4\cdot \sqrt{2}):4$
$(2\cdot\sqrt{50} + 7\cdot \sqrt{50}):5$
$14$
$10$
$2$
$6$
$7\sqrt{n}$
$2$
$\sqrt{2}/2=1/\sqrt{2}$
$9\sqrt{2}$
Quiz 1 kahoot

Make learning awesome. Play against your colleagues.
Aufgabe 5 Vorfaktor
Bringe den Vorfaktor unter die Wurzel.
$6\sqrt{3}$
$4\sqrt{5}$
$4\sqrt{3}$
5$\sqrt{3}$
$8\cdot \sqrt{9}$
$2\sqrt{3}$
$\sqrt{108}$
$\sqrt{80}$
$\sqrt{48}$
$\sqrt{75}$
$\sqrt{576}=24$
$\sqrt{12}$
Quiz 2 Bingo - Differenziertes lernen

Schreibe folgende Zahlen in dein Heft. Wähle dabei deine eigene Reihenfolge der Zahlen.
Nun werden Aufgaben zu den Zahlen gestellt. Die richtige Antwort musst du markieren.
Sollte eine Reihe oder Spalte markiert sein darfst du BINGO rufen. Derjenige der zuerst Bingo ruft und dessen Ergebnisse stimmen gewinnt.
Idee: B. Gams
Wortliste und Satzbausteine
| das Schokoladenstück, -e | Teil einer Schokolade |
| das Quadrieren, - | Multiplieziert man eine Zahl mit sich selbst erhält man das Quadrat der Zahl. $2\cdot 2=2^2=4 |
| das Wurzelziehen, - | Die Wurzel aus 4 ist gleich 2: $\sqrt{4}=2$. Dabei ist 2 der Wert der Wurzel. Die Berechnung des Wurzelwertes bezeichnet man als Wurzelziehen oder auch radizieren. Der Wert der Wurzel entspricht der Zahl, welche mit sich selbst multipliziert den Wert unter der Wurzel gibt. |
| die Quadratwurzel, -n | Eine andere Bezeichnung für radizieren oder wurzelziehen. |
| der Radikant, -en | die Zahl unter der Wurzel |
| die Kantenlänge, -n | die Länge einer Seite |
| die Fläche, -n | die Größe einer begrenzenten Ebene, auch Flächeninhalt |