Kerze

Lineare Funktionen

Lineare Funktion kommen in vielen Anwendungen zum Tragen. Mit Ihnen kann man beispielsweise das Abbrennen einer Kerze oder auch die Kosten einer Taxifahrt beschreiben. Auf diesen Seiten findest du einige einfache Übungsaufgaben dazu.

Funktionsschaubild einer Geraden
Geradengleichung: $$f(x)=mx+b$$

$m=\frac{\Delta y}{\Delta x}$   Steigung

$b$   y-Achsenabschnitt

Interessantes: Man verwendet $\Delta y$ (griech. D) für die Distanz in y-Richtung. Bewegt man sich dabei vom Startpunkt in Pfeilrichtung ist die Distanz positiv, in entgegengesetzte Richtung ist die Distanz negativ.

Aufgabe 1

Die Abbildung zeigt die Schaubilder zweier linearer Funktionen.

  1. Bestimme die Funktionsgleichungen der beiden Geraden.
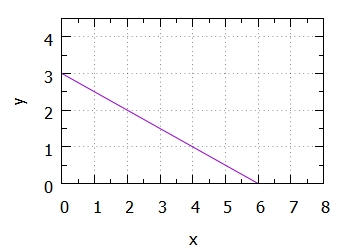
  2. Zeichne die Funktion $f(x)=-1/2x+3$.

  1. $f(x)=1/4x+2$

    $g(x)=-1/2x+1$

  2. Schaubild der Funktion $f(x)=-1/2x+3$:

    Gerade
Gerade


Aufgabe 2 Funktionsterme

Autoren: D. Supper | DFU und binnendifferenziert

Wähle aus den folgenden Aufgaben eine aus, welche Dein Interesse am meisten weckt.

Eine Schraubenfeder hat unbelastet eine Länge von 2 cm. Pro 100 g Gewicht ändert sich die Länge um 0,5 cm.

  1. Lege eine Wertetabelle für Gewichte (x-Wert) von 0 bis 600 g an.
  2. Zeichne das Schaubild der Funktion.
  3. Bestimme die Funktionsgleichung.
  4. Berechne die Federlänge und Auslenkung, wenn man die Feder mit 1,3 kg belastet.
  5. Die Feder darf ohne Schaden zu nehmen maximal 20 cm ausgelenkt werden. Berechne die maximale Federbelastung.
Schraubenfeder

verschneites Auto

Ein Führerschein kostet eine Grundgebühr von 150 EUR. Pro Fahrstunde wird ein Preis von 25 EUR fällig

  1. Lege eine Wertetabelle für 0 bis 6 Fahrstunden (x-Wert) an.
  2. Zeichne das Schaubild der Funktion.
  3. Bestimme die Funktionsgleichung.
  4. Berechne die Kosten für 17 Fahrstunden.
  5. Georg stehen maximal 710 EUR zur Verfügung. Berechne die maximale Anzahl an möglichen Fahrstunden.

Beim Tauchen ist man einem großen Wasserdruck ausgesetzt. Bei einer Tauchtiefe von 21 m kann man pro Minute nur 5 m auftauchen.

  1. Lege eine Wertetabelle für die Auftauchdauer (x-Wert) in Minuten und die Tauchtiefe in Meter an.
  2. Zeichne das Schaubild der Funktion.
  3. Bestimme die Funktionsgleichung.
  4. Berechne die Tiefe nach 2,5 Minuten.
  5. Bestimme die Auftauchdauer.
Korallenriff mit Fischen

Die Schraubenfeder

  1. Wertetabelle:
    Gewicht in g 0 100 200 300
    Länge in cm 2 3 4 5
  2. Schaubild der Funktion:
    Schaubild einer linearen Funktion
  3. Funktionsgleichung: $f(x)=0,01x+2$
  4. Federlänge und Auslenkung bei 1,3 kg Belastung: $f(1300)=15
  5. maximale Federbelastung: Löse die Gleichung $20=0,01x+2$

Der Führerschein:

  1. Wertetabelle:
    Anz. Stunden 0 1 2 3
    Kosten in EUR 150 175 200 225
  2. Schaubild der Funktion:
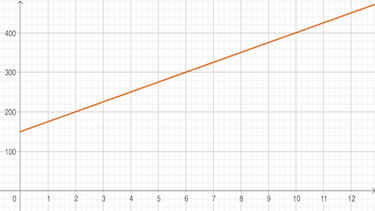
    Schaubild einer linearen Funktion
  3. Funktionsgleichung: $f(x)=25x+150$
  4. Kosten für 17 Fahrstunden: $f(17)=575$ EUR
  5. maximale Anzahl an Fahrstunden: Löse die Gleichung $710=25x+150$

Das Tauchen

  1. Wertetabelle:
    Zeit 0 1 2 3
    Länge in cm -21 -16 -11 -6
  2. Schaubild der Funktion:
    Schaubild einer linearen Funktion
  3. Funktionsgleichung: $f(x)=5x-21$
  4. Tiefe nach 2,5 Minuten: $f(2,5)=-8,5$
  5. Auftauchdauer: Löse die Gleichung $0=5x-21$

Aufgabe 3

Gegeben ist folgende Funktion: $f(x)=\frac{4}{5}x-2$

  1. Berechne den Schnittpunkt Sx mit der x-Achse.
  2. Berechne den Schnittpunkt Sy mit der y-Achse.
  3. Zeichne das Schaubild der Funktion.

  1. Schnittpunkt mit der x-Achse: Sx(2,5|0)

  2. Schnittpunkt mit der y-Achse: Sy(0|-2)

  3. Schaubild der Funktion $f(x)=\frac{4}{5}x-2$:

    Gerade


Aufgabe 4

Ordne eine Funktionsgleichung dem Schaubild zu.

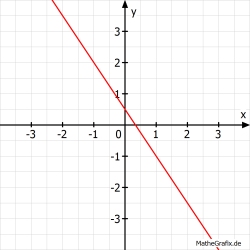
Gerade

Ordne eine Funktionsgleichung dem Schaubild zu.

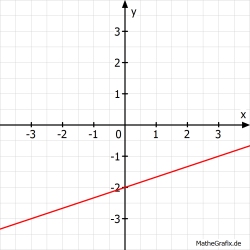
Gerade

Ordne eine Funktionsgleichung dem Schaubild zu.

Gerade

Ordne eine Funktionsgleichung dem Schaubild zu.

Gerade


Aufgabe 5

Bestimme die Funktionsgleichung rechnerisch.

  1. Die Gerade geht durch den Punkt A(5|3) und hat den y-Achsenabschnitt b = 2.
  2. Die Gerade geht durch den Punkt A(2|4) und hat den y-Achsenabschnitt b = 1.
  3. Die Gerade geht durch den Punkt A(4|-2) und hat den y-Achsenabschnitt b = 5.
  4. Die Gerade geht durch den Punkt A(½|3) und hat den y-Achsenabschnitt b = -2.
  5. Die Gerade geht durch den Punkt A(¾|4) und hat den y-Achsenabschnitt b = 0.
  6. Die proportionale Gerade geht durch den Punkt A(4|2).
  7. Die Gerade geht durch den Punkt A(-2|1) und B(2|3).

  1. mit $A(5|3)$ und $b=2$ einsetzen in $y=mx+b$ ⇔ $3=m\cdot 5+2 $ ⇔ $ m=1/5$

    Geradengleichung: $f(x)=\frac{1}{5}x+2$

    Schaubild einer lineare Funktione

  2. Geradengleichung: $f(x)=\frac{3}{2}x+1$

  3. Geradengleichung: $f(x)=-\frac{7}{4}x+5$

  4. Geradengleichung: $f(x)=10x+-2$

  5. Geradengleichung: $f(x)=\frac{16}{3}x$

  6. Geradengleichung: $f(x)=\frac{1}{2}x$ (Hinweis: Eine proportionale Funktion geht immer durch den Koordinatenursprung.)

  7. mit $A(-2|1)$ und $B(2|3)$ folgt:
    $m=\frac{\Delta y}{\Delta x}=\frac{3-1}{2-(-2)}=\frac{2}{4}=0,5$
    mit $B(2|3)$ und $m=0,5$ einsetzen in $y=mx+b$ ⇔ $3=0,5\cdot 2+b$ ⇔ $ b=2$
    folgt die Geradengleichung: $f(x)=0,5x+2$



Wortliste und Satzbausteine



die lineare Funktion, -en eine Funktion mit der Form: $f(x) = mx + b$, mit $a$ ungleich Null
der Funktionswert $f(x)$, -e der zugehörige Wert zu der Funktionsstelle $x$.
die Gerade, -n das Schaubild/der Graf der linearen Funktion, man erhält diesen indem man die einzelnen Wertepaare aus Funktionstelle und Funktionswert in einem Koordinatensystem aufträgt.
die Nullstelle, -n der Schnittpunkt mit der x-Achse
der y-Achsen­abschnitt $b$, -e der Schnittpunkt der Geraden mit der y-Achse. Man erhält ihn indem man $f(0)$ berechnet
die Steigung $m$, -en ein Maß für die Steilheit/Anstieg einer Geraden: $m=\frac{\Delta y}{\Delta x}$
die Distanz $\Delta$, -en $\Delta y$ - Distanz in y-Richtung, $\Delta x$ - Distanz in x-Richtung
der Schnittpunkt zweier Geraden Gemeinsamer Punkt von Gerade 1 und Gerade 2
© mylime.info