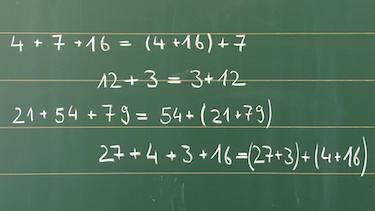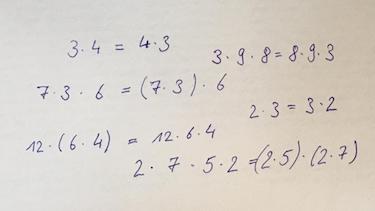Regenbogen

Mit natürlichen Zahlen rechnen

Etwa 2,4 Millionen Liter Wasser stürzen jede Sekunde die Niagarafälle hinab. Möchte man wissen wieviel Liter das in einer Minute sind, muss man mit großen Zahlen rechnen können. Genau das lernst du in diesem Kapitel.

1 Addieren und subtrahieren
addieren, man addiert $7$ $+$ $3$
die Summe, -n $7 + 3$
der Summand, -en $7$ $+$ $3$
sub­trahieren, man sub­trahiert $5$ $-$ $4$
die Differenz, -n $5 - 4$
der Minuend, -en $5$ $-\:4$
der Sub­trahend, -en $5\:-$ $4$

Eric fährt in 3 Etappen zum Doi Suthep. Insgesamt fährt er 20 km.
Etappe 1 (Zoo - Wat Suthep): 11 km
Etappe 2 (Wat Suthep - Bhuping Palace): 4 km
Etappe 3 (Bhuping Palace - Doi Suthep):

Berechne die Länge der ersten beiden Etappen und die Entfernung der letzten Etappe:
Etappe 1+2: 11 + 4 = 15 km
Etappe 3: 20 - 15 = 5 km

2 Zusammenhang zwischen Addition und Subtraktion
Bratwürstchen

Auf dem diesjährigen Weihnachtsfest wurden 650 Würstchen verkauft, 99 mehr als letztes Jahr.
Getränke wurden 420 Flaschen verkauft, 40 weniger als letzes Jahr.
Wie kann man die Zahlen aus dem Vorjahr berechnen?

$\require{extpfeil}\Newextarrow{\xtofrom}{10,10}{0x21C4}$ ${551} \xtofrom[\text{-99}]{\text{+99}} 650$      $460 \xtofrom[\text{+40}]{\text{-40}} 420$


1 Die Addition einer Zahl wird durch die Subtraktion dieser Zahl rückgängig gemacht.
2 Die Subtraktion einer Zahl wird durch die Addition dieser Zahl rückgängig gemacht.

3 Terme und Klammern
Laufschuhe

Ein Paar Laufschuhe wurde von 230 EUR um 40 EUR reduziert. Zu Weihnachten gibt es nochmal zusätzlich einen Rabat von 7 EUR. Berechne den Preis.

Es gibt zwei Rechenwege:
$230-(40+7)=230-47=183$ €
$230-40-7=183$ €
Ein Minuszeichen vor einer Klammer dreht alle Vorzeichen in der Klammer um.

Geschachtelte Klammern:
$230-\left[ 30-(2+3)\right]=230-\left[ 30-5\right]$
 Innere Klammer zuerst.

4 Additionsgesetze
Summen

Kommutativgesetz (Vertauschungsgesetz)
$7+13=13+7$
$a+b=b+a$
In einer Summe darf man die Summanden vertauschen.

Assoziativgesetz (Verbindungsgesetz)
$7+13+12=(7+13)+12$
$(a+b)+c=a+(b+c)=a+b+c$
In einer Summe mit 3 und mehr Summanden darf man beliebig Klammern setzen.

5 Die schriftliche Addition und Subtraktion
Flugzeug

Von Chiang Mai nach Bangkok fliegt man 599 km, von Bangkok nach Berlin 8598 km.
Fliegt man von Chiang Mai über Doha nach Berlin sind es 9311 km.

$\begin{align} 599 && 9311&&\\ \underline{+8598} && \:\:\:\: \underline{-9197}&&\\ 9197&& 114&& \end{align}$

Von Chiang Mai nach Berlin fliegt man 9197 km. Die Strecke über Doha ist 114 km länger.
Merke: Subtrahiert man zwei Werte von einer Zahl, kann man die Summe der beiden Werte subtrahieren.

6 Multiplizieren und Dividieren
multi­plizieren, man multi­pliziert $5$ $\cdot$ $2$
das Pro­dukt, -e $5 \cdot 2$
der Faktor, -en $5$ $\cdot$ $2$
divi­dieren, man divi­diert $9$ $:$ $3$
der Quo­tient, -en $9 : 3$
der Divi­dend, -en $9$ $: 3$
der Divi­sor, -en $9 :$ $3$

Natascha streicht eine Fläche von 3 m x 4 m. Kais Fläche ist 5mal größer, Erics nur halb so groß.

Berechne die Flächen.
Natascha: 3 ⋅ 4 = 12 m2
Kai: 5 ⋅ 12 = 60 m2
Eric: 12 : 2 = 6 m2

7 Zusammenhang Multiplikation und Division
Känguru

Ein Känguru erreicht beim Springen eine Geschwindigkeit von bis zu 54 km/h. Das ist 3mal schneller als eine Honigbiene und 3mal langsamer als ein Barrakuda.
Berechne die Geschwindigkeiten der anderen Tiere.

$\require{extpfeil}\Newextarrow{\xtofrom}{10,10}{0x21C4}$ ${54} \xtofrom[\text{:3}]{\cdot 3} 162$      $54 \xtofrom[\cdot 3]{:3} 18$

1 Die Multiplikation mit einer Zahl wird durch die Division mit dieser Zahl rückgängig gemacht.
2 Die Division durch eine Zahl wird durch die Multiplikation mit dieser Zahl rückgängig gemacht.

8 Terme und Rechenregeln Multiplikation
Bienenfresser

Ein Bienenfresser fängt 22 Mosquitos und 8 Fliegen. Das wiederholt er 5mal.

Es gibt zwei Rechenwege:
$5\cdot(22+8)=5\cdot 30= 150$ Insekten
$5\cdot(22+8)=5\cdot 22 +5\cdot 8=110+40$
Beachte: $200-5\cdot(22+8)=200-150$

Klammer vor Punkt vor Strich:

  1. Klammern werden zuerst gerechnet,
  2. Punkt- vor Strichrechnung,
  3. wir rechnen von links nach rechts.

9 Rechengesetze Multiplikation
Rechengesetze

Kommutativgesetz (Vertauschungsgesetz)
$5\cdot 12=12\cdot 5$
$a\cdot b=b\cdot a$
In einem Produkt darf man die Faktoren vertauschen.

Assoziativgesetz (Verbindungsgesetz)
$5\cdot 12\cdot 2=(5\cdot 12)\cdot 2$
$(a\cdot b) \cdot c=a \cdot (b \cdot c)=a\cdot b\cdot c$
In einem Produkt mit 3 und mehr Faktoren darf man beliebig Klammern setzen, bzw. weglassen.

10 Variablen und Gleichungen
Würfel

Man gewinnt, wenn man die Augenzahl mit sich selbst multipliziert und 10 addiert, genauso groß ist, wie das 7fache der Augenzahl. Verwende für das Spiel einen Würfel.

$\text{Augenz.} \cdot \text{Augenz.} + 10 = 7 \cdot \text{Augenz.}$
 $x\cdot x + 10= 7 \cdot x$

Wenn eine Zahl einen unterschiedlichen Wert haben kann, benötigen wir hierfür einen Platzhalter. Dies kann ein Buchstabe oder auch ein Wort sein und wird als Variable bezeichnet. Enthält ein Term ein Gleichheitszeichen sprechen wir von einer Gleichung.

11 Die schriftliche Multiplikation und Division
Niagrafälle

2.400.000 Liter Wasser stürzen jede Sekunde die Niagarafälle hinab. Zeige, dass die Menge in einer Minute 144 Millionen Liter beträgt.
An manchen Tagen sieht man bis zu 552 Wildgänse über den Fluß fliegen. Zeige, dass im Durchschnitt 23 Wildgänse pro Stunde fliegen.

$\begin{align} \underline{2.400.000 \cdot 60} && \:\:\:\: 552 : 24=23 \\ 144.000.00 \:\: && \underline{-48} \qquad \qquad \\ \underline{+\qquad \quad \:\:0} && 72 \:\:\:\quad \qquad \\ 144.000.000 && \underline{-72}\:\:\:\quad \qquad\\ && 0 \:\:\:\quad \qquad\\ \end{align}$



Aufgabe 1 Entfernungen berechnen.

Wenn man von Samoeng über Chiang Mai nach Bangkok fährt legt man 757 km zurück.

  1. Berechne die Enternung von Chiang Mai nach Samoeng.
  2. Berechne die Entfernung von Chiang Mai nach Bangkok.
  3. Erfinde eine eigene Aufgabe.
Sternhimmel über Westaustralien

  1. Von Chiang Mai nach Samoeng sind es 52 km.
  2. Von Chiang Mai nach Bangkok sind es 705 km.

Aufgabe 2 Die Zahlenpyramide - Addition und Subtraktion

Rechne mit benachbarten Zahlen.

Addition

$$\begin{equation*} \begin{array}{ccccccccc} & & & & &87 & & & &\\ & & & & \text{__} & & \text{__} & & &\\ & & &23 & &21 & & \text{__} & &\\ & &12 & & \text{__} & & \text{__} & & \text{__} &\\ & \text{__} & &4 & & \text{__} & & \text{__} & & \text{__} \\ \end{array} \end{equation*} $$

Subtraktion

$$\begin{equation*} \begin{array}{ccccccccc} & & & & &2 & & & &\\ & & & &\text{__} & &\text{__} & & &\\ & & &\text{__} & &\text{__} & &\text{__} & &\\ & &36 & &\text{__} & &15 & &\text{__} &\\ &99 & &\text{__} & &40 & &\text{__} & &\text{__}\\ \end{array} \end{equation*} $$

Addition

$$\begin{equation*} \begin{array}{ccccccccc} & & & & &87 & & & &\\ & & & &44 & &43 & & &\\ & & &23 & &21 & &22 & &\\ & &12 & &11 & &10 & &12&\\ &8 & &4 & &7 & &3 & &9\\ \end{array} \end{equation*} $$

Subtraktion

$$\begin{equation*} \begin{array}{ccccccccc} & & & & &2 & & & &\\ & & & &5 & &3 & & &\\ & & &13 & &8 & &5 & &\\ & &36 & &23 & &15 & &10 &\\ &99 & &63 & &40 & &25 & &15\\ \end{array} \end{equation*} $$

Aufgabe 3 Gewicht, Zeit und Strecke

Berechne dei fehlenden Größen.

Nutella Gläser

Ein Nutella­ Größe L wiegt 250 g. Es ist 200 g schwerer als Größe S und 230 g leichter als Größe XL.

  1. Eine Nutella L wiegt 250 g. Sie ist 225 g schwerer als S und 230 g leichter als XL. Bestimme die Gewichte aller drei Gläser.

  2. Ein Flug von Bangkok nach Frankfurt dauert 10,5 Stunden. Er ist 8,5 Stunden länger als nach Krabi und 6,5 Stunden kürzer als nach New York.

  3. Ein Marathon ist 42,2 km lang. Er 23,8 km kürzer als ein Ultra und 32,2 km länger als ein Minimarathon.

  4. Tim wiegt 47 kg. Das ist 12,3 kg leichter als Tom und 24,3 kg schwerer als Ted.


  1. Nutella S: 25 g
    Nutella XL: 480 g

  2. Flug BKK-Krabi: 2 h
    Flug BKK-New York: 17 h

  1. Ultra: 66 km
    Minimarathon: 10 km

  2. Tom: 59,3 kg
    Ted: 22,7 kg


Aufgabe 4 Klammern und Terme

Berechne den Wert der Terme

  1. $1220-(200+20)$

  2. $1220-200+20$

  3. $1200-(133+67)$

  4. $600-(400-25)$

  5. $600-400-25$

  1. $1230-\left[ 60-(20+30)\right]$

  2. $(27-24)+(12+3)$

  3. $123+\left[ 30-(20+3)\right]=130$

  4. $7.605.000-\left[ 3000-(200+700)\right]$

  5. $400.000-\left[ 15.000-(2000+200)\right]$


  1. $1220-(200+20)=1000$

  2. $1220-200+20$=1040

  3. $1200-(133+67)=1000$

  4. $600-(400-25)=225$

  5. $600-(225-25)=400$

  1. $1230-\left[ 60-(20+30)\right]=1220$

  2. $(27-24)+(12+3)=18$

  3. $123+\left[ 30-(20+3)\right]=130$

  4. $=7.603.000$

  5. $=387.200$


Aufgabe 5 Addition und Subtraktion


  1. $\begin{align} 699 &&\\ \underline{+4598} &&\\ \end{align}$

  2. $\begin{align} 99 &&\\ 212 &&\\ \underline{+9876} &&\\ \end{align}$

  1. $\begin{align} 9999 &&\\ \underline{-598} &&\\ \end{align}$

  2. $\begin{align} 12399 &&\\ -476 &&\\ \underline{-3281} &&\\ \end{align}$

  1. $\begin{align} 99999 &&\\ \underline{-88881} &&\\ \end{align}$

  2. $\begin{align} 1555555 &&\\ -1111 &&\\ \underline{-4321} &&\\ \end{align}$

  1. $\begin{align} 845845 &&\\ \underline{-2121} &&\\ \end{align}$

  2. $\begin{align} 64329 &&\\ -50111 &&\\ \underline{-8743} &&\\ \end{align}$
  1. Auf der Tropeninsel Kho Phi Phi werden in dem Resort "Traumstrand" in der Hauptsaison 224.350 Übernachtungen gezählt. In der Vorsaison waren es 65.400 und in der Nachsaison 43.900. Berechne die Anzahl an Gästen bis 500.000 Übernachtungen erreicht sind.


  1. $5.297$

  2. $10.187$

  1. $9.401$

  2. $8.642$

  1. $91.118$

  2. $1.550.123$

  1. $843.724$

  2. $5.475$

  1. $166.350$

Aufgabe 6 Multiplizieren und Dividieren

Finde die Zahl.

  1. $\require{extpfeil}\Newextarrow{\xtofrom}{10,10}{0x21C4}$ ${36} \xtofrom[\text{}]{} 6$

  2. $\require{extpfeil}\Newextarrow{\xtofrom}{10,10}{0x21C4}$ $12 \xtofrom[]{} 60$

  3. $\require{extpfeil}\Newextarrow{\xtofrom}{10,10}{0x21C4}$ ${144} \xtofrom[\text{}]{} 12$

  4. $\require{extpfeil}\Newextarrow{\xtofrom}{10,10}{0x21C4}$ $17 \xtofrom[]{} 51$

Fülle die Lücken aus.

  1. $\text{__} \cdot 12 = 60$

  2. $60 \cdot \text{__}= 0$

  3. $\text{__} : 10 = 49$

  4. $0 : \text{__}= 0$


Finde die Zahl.

  1. $\require{extpfeil}\Newextarrow{\xtofrom}{10,10}{0x21C4}$ ${36} \xtofrom[\text{:6}]{\cdot 6} 6$

  2. $\require{extpfeil}\Newextarrow{\xtofrom}{10,10}{0x21C4}$ $12 \xtofrom[\cdot 5]{:5} 60$

  3. $\require{extpfeil}\Newextarrow{\xtofrom}{10,10}{0x21C4}$ ${144} \xtofrom[\text{:12}]{\cdot 12} 12$

  4. $\require{extpfeil}\Newextarrow{\xtofrom}{10,10}{0x21C4}$ $17 \xtofrom[\cdot 3]{:3} 51$

Fülle die Lücken aus.

  1. $\underline{5} \cdot 12 = 60$

  2. $60 \cdot \underline{0}= 0$

  3. $\underline{490} : 10 = 49$

  4. $0 : \underline{10}= 0$


Aufgabe 7 Klammern und Terme

Berechne. Zeige dabei den Rechenweg auf.

  1. $3+4 \cdot 12 - 1$

  2. $100-17\cdot 2+9:3$

  3. $(38+7):(7-2)$

  4. $(6+7\cdot 2)-(10-5)$

  1. $(7+14)\cdot 2 : 2 + (38 -26)$

  2. $15:5 \cdot [8 \cdot (6:2)]$

  3. $23-[5\cdot 3+2\cdot (7-3)]=23-(15+8)=0$

  4. $(18-7)\cdot 4 + (27+4)$

  1. $3+4 \cdot 12 - 1=3+48-1=50$

  2. $100-17\cdot 2+9:3=89$

  3. $(38+7):(7-2)=9$

  4. $(6+7\cdot 2)-(10-5)=15$

  1. $(7+14)\cdot 2 : 2 + (38 -26)=33$

  2. $15:5 \cdot [8 \cdot (6:2)]=72$

  3. $=23-(15+8)=0$

  4. $(18-7)\cdot 4 + (27+4)=75$



Entspann dich erst mal ...

Fakten über den Mond

23 Fakten über den Mond.

Aufgabe 8 Rechen­gesetzte Mulitplikation

Der Mond hat einen Durchmesser von etwa 3500 km. Die Entfernung zur Erde beträgt etwa das 110fache. Die Erde hat etwa den 4fachen und der Mars etwa den doppelten Durchmesser des Mondes. Die Sonne hat einen Durchmesser von ca. 1.400.000 km.

  1. Berechne den Abstand zwischen Erde und Mond.
  2. Berechne den Durchmesser von Erde und Mars.
  3. Berechne wieviel mal die Sonne größer ist als die Erde.
Blutmond

  1. Abstand zwischen Erde und Mond: 385.000 km
  2. Durchmesser von Erde und Mars: 14.000 km
  3. Berechne wieviel mal die Sonne größer ist als die Erde: 400 mal


Aufgabe 9 Zeitangaben

Berechne die Zeitangaben in Sekunden und Stunden.

  1. $90\:\text{min}$
  2. $30\:\text{min}$
  3. $180\:\text{min}$
  1. $600\:\text{min}$
  2. $420\:\text{min}$
  3. $240\:\text{min}$
  1. $90\:\text{min}=90:60=1,5\:\text{h}=5.400\:\text{s}$
  2. $30\:\text{min}=0,5\:\text{h}=1.800\:\text{s}$
  3. $180\:\text{min}=3\:\text{h}=10.800\:\text{s}$
  1. $600\:\text{min}=10\:\text{h}=36.000\:\text{s}$
  2. $420\:\text{min}=7\:\text{h}=25.200\:\text{s}$
  3. $240\:\text{min}=4\:\text{h}=14.400\:\text{s}$

Aufgabe 10 Variablen

Würfel

Finde den richtigen Wert der Variable $x$ heraus.

  1. Man gewinnt, wenn die Augenzahl $x$ mit 8 addiert genauso groß ist, wie das 9fache der Augenzahl. Tipp: $x\cdot x +4 = 4x$
  2. Man gewinnt, wenn das Doppelte von Augenzahl $x$ mit 4 addiert genauso groß ist, wie das 6fache der Augenzahl.
  3. Man gewinnt, wenn die Augenzahl $x$ mit sich selbst multipliziert genauso groß ist, wie das 8fache der Augenzahl minus 12.

  1. Augenzahl: $x=1$
  2. Augenzahl: $x=4$
  1. Augenzahl: $x=2$ oder $x=6$

Aufgabe 11 Schriftlich multipli­zieren und divi­dieren

  1. $400 \cdot 12$
  2. $30 \cdot 33$
  3. $180 \cdot 17$
  1. $3600 : 9$
  2. $420 : 12$
  3. $3.664 : 8$
  1. $4.250 \cdot 15$
  2. $7.303 \cdot 69$
  3. $18.845 \cdot 17$
  1. $3625 : 25$
  2. $8094 : 19$
  3. $7777 : 7$

  1. $400 \cdot 12=4800$
  2. $30 \cdot 33=990$
  3. $180 \cdot 17=3.060$
  1. $3600 : 9=400$
  2. $420 : 12=35$
  3. $3.664 : 8=458$
  1. $4.250 \cdot 15=63.750$
  2. $7.303 \cdot 69=503.907$
  3. $18.845 \cdot 17=320.365$
  1. $3625 : 25=145$
  2. $8094 : 19=426$
  3. $7777 : 7=1.111$

Wortliste und Satzbausteine



addieren, man addiert $7$ $+$ $3$
die Summe, -n $7 + 3$
der Summand, -en $7$ $+$ $3$
sub­trahieren, man sub­trahiert $5$ $-$ $4$
die Differenz, -n $5 - 4$
der Minuend, -en $5$ $-\:4$
der Sub­trahend, -en $5\:-$ $4$
multi­plizieren, man multi­pliziert $5$ $\cdot$ $2$
das Pro­dukt, -e $5 \cdot 2$
der Faktor, -en $5$ $\cdot$ $2$
divi­dieren, man divi­diert $9$ $:$ $3$
der Quo­tient, -en $9 : 3$
der Divi­dend, -en $9$ $: 3$
der Divi­sor, -en $9 :$ $3$
etwas rück­gängig machen ctrl + Z
das Vorzei­chen Jede Zahl kann ein positives oder negatives Vorzeichen haben: $+6$ oder $-6$
etwas aufzei­gen etwas deutlich machen oder hervorheben
die Variable, -en ein Platzhalter für eine beliebige Zahl: $x, y, ...$
die Gleichung, -en ein Term mit Gleichheitszeichen: $x+4=2$
© mylime.info