Zuordnungen und Funktionen
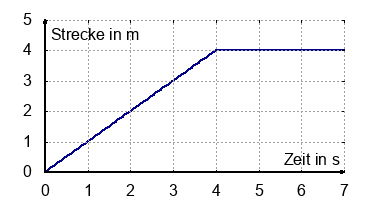
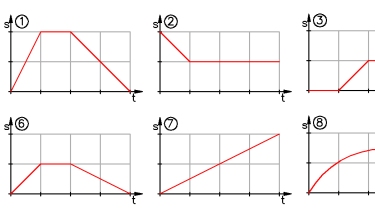
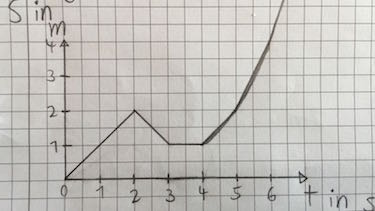
Experiment 1 Zeit-Weg-Diagramm
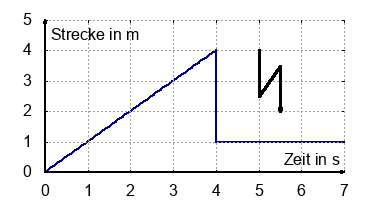
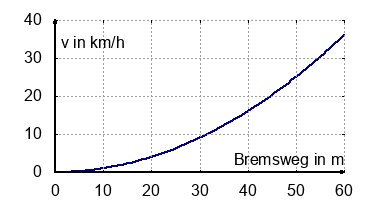
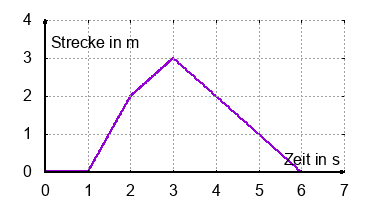
Die Abbildung zeigt einen Ausschnitt von Zeit-Weg-Diagrammen.
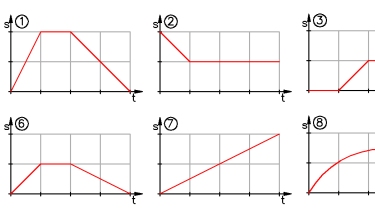
Zeichne 10 solche t-s-Diagramme an die Tafel.
- Einer von Euch schreitet nun im Raum den Weg eines der Diagramme auf einem Laufsteg mit Startpunkt zweimal ab. Dazu klatscht er bei jeder Bewegungsänderung in die Hand.
- Woran erkennt man das richtige t-s-Diagramm?
- Hast Du es herausgefunden, dann lehne dich entspannt zurück.
- Gebt per Handzeichen euer Votum ab. Einer der es richtig hatte darf nun an dieser Stelle ein neues Diagramm zeichnen und ein neues Zeit-Weg-Diagramm ablaufen.
Aufgabe 2 tabellarische Zuordnung
Die Paketpreise der Post sind abhängig vom Gewicht. Im Folgenden ist eine tabellarische Zuordnung dargestellt Gewicht und Preis.
| Gewicht in kg | 3 | 6 | 8 | 10 | 12 |
| Preis in EUR | 3,50 | 7 | 9,50 | 12 | 14,50 |
- Trage die Werte in ein Gewicht-Preis-Diagramm.
- Zeichne ein Diagramm, bei dem der erste Preis von 0 bis 3 kg gilt, der zweite Preis über 3 - 6 kg u.s.w.
- Notiere eine tabellarische Zuordnung für eine Taxifahrt, wenn neben einer Grundgebühr von 3 EUR, jeder km 2,50 EUR kostet.

- Gewicht-Preis-Diagramm:
- Zeichne ein Diagramm, bei dem der erste Preis von 0 bis 3 kg gilt, der zweite Preis über 3 - 6 kg u.s.w.:
- tabellarische Zuordnung Taxifahrt:
Entfernung in km 0 1 2 4 6 Preis in EUR 3 5,5 8 13 18
Aufgabe 3 Texte und Zuordnung
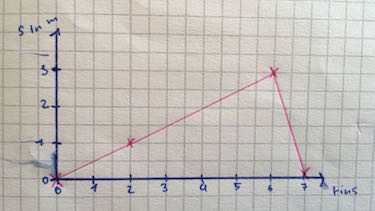
Zeichne die Zuordnung in ein Zeit-Weg-Diagramm.
Eine Biene fliegt 1 m in 2 s, dann 2 m in 4 s. Dann geht sie in 1 s zum Start zurück.
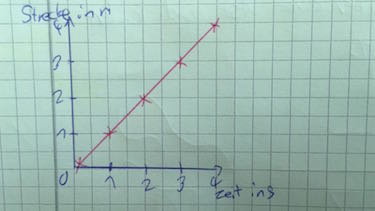
Tom läuft in 4 s 4 m.
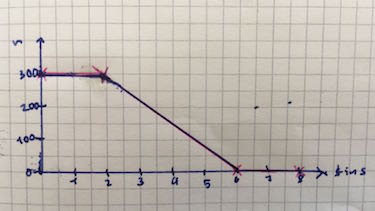
Ein Flugzeug fliegt in 300 m Höhe für 2 s. Dann braucht es 4 s für die Landung und bleibt 2 s stehen.
Jörn geht in 2 s 2 m. In der nächsten Sekunde geht er einen Meter zurück und bleibt dann eine Sekunde stehen. Abschließend wird er immer schneller.
Erfinde eigene Aufgaben.
Aufgabe 4 proportionale Zuordnung

- Für 1 EUR erhält Andrea THB 37,5. Berechne wie viel THB Andrea für 5 EUR, 10 EUR, 20 EUR, 50 EUR und 100 EUR erhält.
- Zeichne die proportionale Zuordnung in ein Diagramm.
- Sray hat THB 1200 und möchte nach Europa. Berechne wie viele Euro sie dafür bekommt.
-
EUR 1 5 10 20 ... THB 37,5 187,5 375 750 ... -
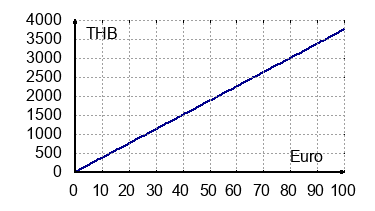
- Sray erhölt 1200/37,5 = 32 EUR
Aufgabe 5 proportionale und umgekehrt proportionale Zuordnungen
Gib Beispiele aus der Praxis an, in denen die Zuordnung proportional oder umgekehrt proportional ist.
Proportionale Zuordnungen:
- Die doppelte Menge an Hühnern, legen die doppelte Menge Eier. (Sylvia)
- Wenn man 2 Windräder besitzt, hat man doppelt so viel Energie und benötigt 2mal so viel Material. (Bennet)
- ...
Umgekehrt proportionale Zuordnungen:
- Hat man doppelt so viel Hausaufgaben, halbiert sich die Motivation. (Jannik)
- ...
Proportionale Zuordnungen:
- Wenn ich doppelt so viel Esse, nehme dich doppelt so viel Kalorien zu mir und verbrauche das zweifache an Essen. (Noah)
- Wenn man doppelt so viel arbeitet, bekommt man doppelt so viel Lohn. (Nathanael)
- Die dreifache Menge an Füßen, benötigt 3mal so viel Schuhe. (Mercy)
- Die 2fache Menge an Klassenarbeiten, bedeutet die doppelte Lernzeit. (Rachel)
- Zwei Fußbälle sind doppelt so teuer, als einer. (Ginger)
- Für die 2fache Menge an Kindern, benötigt das doppelte an Schulgeld. (Sukanya)
- Die vierfache Menge an Stühlen, verbraucht viermal so viel Platz. (William)
- Doppelt so viel schreiben, benötigt das 2fache Menge an Papier. (Leo)
Umgekehrt proportionale Zuordnungen:
- Hat man doppelt so viel Hausaufgaben, halbiert sich die Motivation. (Jannik)
- Wenn 1 Arbeiter 4 Tage braucht um eine Mauer zu bauen, benötigen 2 Arbeiter nur 2 Tage.
- Wenn eine Person 12 Fantaflaschen hat, reicht es bei 3 Personen für 4 Fantaflaschen.
Aufgabe 6 Wortschatzarbeit
Erstelle eine "word cloud" mit allen wichtigen Fachbegriffen zum Thema Funktionen und Zuordnung. Verwende hierfür den Word Cloud Generator:
Word cloud made with WordItOut
oder ein ähnliches Programm.
Kettenspiel: Einer beginnt und erklärt der Klasse den ersten Begriff. Dann wählt er einen neuen Begriff und gibt das Wort an den nächsten weiter.
Aufgabe 7 proportional und umgekehrt proportional
Welche der Zuordnungen ist proportional, welche umgekehrt proportional?
- Um alle Fenster des Kreuzfahrtschiffs von außen zu reinigen benötigen 3 Arbeiter 14 Tage. Wie lange braucht einer, bzw. 7?
- 3 Arbeiter brauchen 4 Tage um eine Mauer zu bauen. Wie viele Tage brauchen 5 Arbeiter?
- 5 Hühner legen im Schnitt täglich drei Eier. Wie viele Hühner benötigst du, wenn du täglich 21 Eier möchtest?
- Vier Tische haben eine Fläche von 2,5 m2. Wie viele Tische benötigst du für eine Fläche von 12 m2?
- In einem Fantakasten befinden sich 24 Flaschen. Bei drei Gästen kommen auf jeden 8 Flaschen. Wie viele Flaschen kommen auf 5, 6, 10 und 12 Gästen?

- Fensterputzen auf dem Kreuzfahrtschiff: umgekehrt proportionale Zuordnung

- Mauerbau: umgekehrt proportionale Zuordnung

- Hühnereier: proportionale Zuordnung

- Tische: proportionale Zuordnung
$\begin{equation*} \begin{array}{cccc} 4\:Tische &\to& 2,5\:m^2 &|& \cdot 2/5\\ 8/5\:Tische &\to& 1\:m^2 &|& \cdot 12,5\\ 96/5\:Tische &\to& 12\:m^2 && \\ 19,2\:Tische &\to& 12\:m^2 && \\ \end{array} \end{equation*} $
- Fantakasten: umgekehrt proportionale Zuordnung
$\begin{equation*} \begin{array}{cc} 3\:Gäste &\to& 8\:Flaschen \\ 5\:Gäste &\to& 4,8\:Flaschen \\ 6\:Gäste &\to& 4\:Flaschen \\ 8\:Gäste &\to& 3\:Flaschen \\ 10\:Gäste &\to& 2,4\:Flaschen \\ 12\:Gäste &\to& 2\:Flaschen \\ \end{array} \end{equation*} $
Wortliste und Satzbausteine
| die Zuordnung, -en | Eine mathematische Zuordnung ordnet jedem Wert exakt einen anderen Wert zu. Bspw. kann man auf einer Radtour jeder Zeit einen bestimmten Ort zuordnen. |
| die grafische Zuordnung, -en | Eine grafische Zuordnung, stellt den Zusammenhang zwischen zwei Werten grafisch dar. Dabei wird der eine Wert auf der horizontalen x-Achse und und der zugeordnete Wert auf der vertikalen y-Achse abgetragen. |
| die tabellarische Zuordnung, -en | die Zuordnung wird in einer Tabelle dargestellt |
| das Zeit-Weg-Diagramm, -e | Das Zeit-Weg-Diagramm (auch Zeit-Ort-Diagramm) ist eine grafische Zuordnung. Dabei wird auf der x-Achse die Zeit und auf der y-Achse der Weg (Ort) aufgetragen. |
| das Gewicht-Preis-Diagramm, -e | In der grafischen Zuordnung wird auf der x-Achse das Gewicht und auf der y-Achse der Preis aufgetragen. |
| die proportionale Zuordnung | Bei einer proportionalen Zurordnung gilt: Nimmt man das 2fache, 3fache, ... des x-Wertes, verdoppelt, verdreifacht, ... sich der y-Wert. In der grafischen Zuordnung nennt sich das Schaubild Gerade. |
| die umgekehrt proportionale Zuordnung | Bei einer umgekehrt proportionalen Zurordnung gilt: Nimmt man das 2fache des x-Wertes, halbiert sich der y-Wert. Nimmt man das dreifache des x-Wertes, wird der y-Wert dreimal kleiner. In der grafischen Zuordnung nennt sich das Schaubild Hyperbel. |