Regenbogen

Natürliche Zahlen und Größen

Wie Sonnenstrahlen gibt es auch in der Mathematik Strahlen. Sie haben einen Anfang und gehen in eine Richtung. Dafür benötigen wir einen sicheren Umgang mit großen Zahlen und müssen sie vergleichen können. Darüber hinuas lernst du ein anderes Zahlensystem und den Umgang mit Größen wie Masse, Zeit und Länge kennen.

1 Große Zahlen
Millionen Muscheln

Millionen von kleinen Muscheln liegen in Shellbay in Westaustralien am Strand. Es sind so viele, dass man sie eigentlich gar nicht mehr zählen kann, aber ihre Menge ist natürlich begrenzt und somit kann man die Anzahl als sehr große Zahl darstellen. Für die großen Zahlen hat man folgende Namen festgelegt:

1 Millionen = 1000 Tausender = 1.000.000

1 Milliarde = 1000 Millionen = 1.000.000.000

1 Billionen = 1000 Milliarden = 1.000.000.000

Nenne 3 Beispiele großer Mengen, welche man nicht zählen kann, die endlich sind.

2 Duale Zahlen
Mikrocontrollerboard

In unserem Zehner-Zahlensystem werden 10 Einer zu einem Zehner zusammengefasst, 10 Zehner zu einem Hunderter u.s.w. Deshalb benötigt man zehn Ziffern.

Im Dualsystem werden nur zwei Ziffern verwendet die Null und die Eins. So speichern alle Computer Ihre Daten. Dabei werden zwei einer zu einem Zweier, zwei Zweier zu einem Vierer, zwei Vierer zu einem Achter u.s.w. zusamengefasst:

$1101=8\cdot 1+4\cdot 1+2\cdot 0+1\cdot 1$ $= 13$

Berechne die Zahl 10101 als Dezimalzahl und die Zahl 36 als Dualzahl.

3 Die römischen Geheimzeichen
Marienkirche

Bei Uhren, wie hier bei der Marienkirche in München, werden oft die römischen Zahlenzeichen verwendet. Schon die Römer zählten im Zehnersystem, aber verwendeten eigene Zeichen.

$I=1\:\:$ $V=5\:\:$ $X=10\:\:$ $L=50\:\:$ $C=100\:\:$ $D=500\:\:$ $M=1000$

Achte darauf, welche Folgen es hat, wenn ein niederwertige Zeichen vor einem höherwertigen Zeichen steht. Hier einige Beispiele:
$XIV=10+5-1=14$
$XLVIII=50-10+5+1+1+1$ $=48$
$MCLXXXI=1000+100+50+31$ $=1181$

4 Der Vergleich natürlicher Zahlen
Hongkong

Kennt Ihr die höchsten Gebäude der Welt? Hier in Hongkong steht eines davon. Notiere die 7 höchsten Gebäude in der richtigen Reihenfolge.

Für den Vergleich hat man mathematische Zeichen eingeführt:
$<$ kleiner als,
$>$ größer als,
$=$ gleich.

Hier nun ein paar Beispiel:
$12<13\:\:\:\:$ $5>4\:\:\:\:$ $120<130\:\:\:\:$ $12=12$
Notiere fünf eigene Vergleiche mit großen Zahlen.

5 Der Zahlenstrahl
Zahlenstrahl

Ein Zahlenstrahl hat wie ein Sonnenstrahl einen Anfang und geht in eine Richtung. Die Richtung wird mit einem Pfeil markiert. Die Abstände zwischen den Zahlen machen den Unterschied zwischen den Zahlen leicht wahrnehmbar.

Zahlen die nicht auf dem Zahlenstrahl direkt abgebildet sind können separat sichtbar gemacht werden.

Den Mittelwert zwischen zwei Zahlenangaben ermittelt man, indem man die beiden Zahlen addiert und dann durch 2 teilt.

6 Runden von Zahlen
verschiedene Schuhe

Preise von Waren haben häufig Werte wie 12,99 EUR. Wir runden diese instinktiv auf oder ab um besser vergleichen zu können. Für das Runden von Zahlen gibt es einige logische Regeln.

  1. Ist die Ziffer rechts von der Rundungsstelle größer oder gleich 5, rundet man auf; bei 4 oder kleiner rundet man ab.
  2. Ist die Rundungsstelle eine 9 und die Ziffer rechts von der Rundungsstelle größer oder gleich 5, geht man eine Stelle weiter nach links und entscheidet neu.

Folgende Zahlen solle auf die Zehnerstelle gerundet werden:
$294 \approx 290\:\:$ $297 \approx 300$

7 Länge, Gewicht und Zeit
Burger

100 g oder 200 g Beef Burger. Größen wie Gewicht, Länge oder Zeit haben neben der Zahlenangabe eine Einheit. Dabei gilt:

$$1\:\text{km}=1.000\:\text{m}=1.000.000\:\text{mm}$$ $$1\:\text{kg}=1.000\:\text{g}=1.000.000\:\text{mg}$$ $$1\:\text{h}=60\:\text{min}=3.600\:\text{s}$$

Ideen:
H. Griesel et. al, "Elemente der Mathematik 1 - Baden-Württemberg, Schroedel Verlag, 2013



Aufgabe 1 Große Zahlen

  1. Vervollständige die Tabelle, indem du die Millionen, Tausend, 100er, 10er und 1er an der richtigen Position einträgst.

7 7 0 0 0 0 0 3 77M+3
3M+56T
99T
999M+4T
127T+10

Schreibe als Zahl.

  1. $100T+214$

  2. $27M+14T+3$

  3. $398M+7T+999$

  4. $26Mrd+214M$

  5. $777Mrd+56T+3$

  6. $398B+4T$

Sternhimmel über Westaustralien

  1. Vervollständige die Tabelle.
7 7 0 0 0 0 0 3
3 0 5 6 0 0 0
9 9 0 0 0
9 9 9 0 0 4 0 0 0
1 2 7 0 1 0

Schreibe als Zahl.

  1. $100.214$

  2. $27.014.003$

  3. $298.007.999$

  4. $26.214.000.000$

  5. $777.000.056.003$

  6. $398.000.000.004.000$


Aufgabe 2 Duale Zahlen

Rechne die dezimalen Zahlen in duale Zahlen um.

  1. $8$

  2. $19$

  3. $149$

Rechne die dualen Zahlen in dezimale Zahlen um.

  1. $10010$

  2. $01010$

  3. $111111$


  1. $8=1000$

  2. $19=10011$

  3. $149=10010101$

  1. $10010=18$

  2. $01010=10$

  3. $111111=63$


Aufgabe 3 Römische Zeichen

Marienkirche München

Gib die Zahlen in römischen Zeichen an.

  1. $54$

  2. $542$

  3. $24$

  4. $3458$

  5. Erfinde eine Geschichte mit 10 Zahlenangaben. Schreibe sie auf und gib die Zahlen in römischen Zeichen an.

  1. $54=LIV$

  2. $542=DIXII$

  3. $24=XXIV$

  4. $3458=MMMIDLVIII$

  1. Heute ist der III.IX.MMXVIII. Mein Hamster ...


Aufgabe 4 Vergleiche von Zahlen

Setze das passende Zeichen ein.

  1. $2.341 \:\Box\: 2.342$

  2. $1.200.892 \:\Box\: 1.200.982$

  3. $862.232 \:\Box\: 872.232$

  4. $999.999 \:\Box\: 999.989$

  1. $271.293 \:\Box\: 271.293$

  2. $219.999 \:\Box\: 229.999$

  3. $1.300 \:\Box\: 1.299$

  4. $7.777.777 \:\Box\: 66.666.666$


  1. $2.341 < 2.342$

  2. $1.200.892 < 1.200.982$

  3. $862.232 < 872.232$

  4. $999.999 > 999.989$

  1. $271.293 = 271.293$

  2. $219.999 < 229.999$

  3. $1.300 > 1.299$

  4. $7.777.777 < 66.666.666$


Aufgabe 5 Der Zahlenstrahl

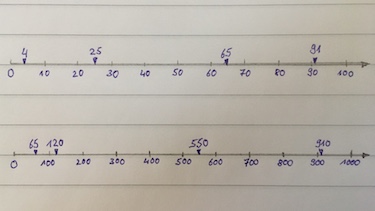
  1. Zeichne einen Zahlenstrahl von 0 bis 100 in 10er Schritten und einen Zahlenstrahl von 0 bis 1000 in 100er Schritten. Trage folgende Zahlen zusätzlich ein: $4$, $65$, $25$ und $91$, $120$, $65$, $550$ und $910$.

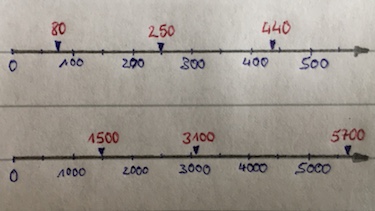
  1. Zeichne einen Zahlenstrahl von 0 bis 500 in 100er Schritten und einen Zahlenstrahl von 0 bis 5000 in 1000er Schritten. Trage folgende Zahlen zusätzlich ein: $80$, $250$, $440$, $1500$, $3100$ und $5700$.

  1. Bestimme die Zahlen, welche in der Mitte von $0$ und $100$, $20$ und $120$ sowie $223$ und $477$ liegen.


  1. Zahlenstrahlen

  1. Zahlenstrahlen


  1. $0$ - $50$ - $100$

    $20$ - $70$ - $120$

    $223$ - $350$ - $477$


Aufgabe 6 Runden

Runde die folgenden Zahlen auf Hundert.

  1. $1.234$

  2. $9.999$

  3. $79$

Runde die folgenden Zahlen auf Zehntausend:

  1. $4.233.909$

  2. $10.000$

  3. $99.999$


  1. $1.234\approx 1.200$

  2. $9.999\approx 10.000$

  3. $79\approx 100$

  1. $4.233.909\approx 4.230.000$

  2. $10.000\approx 10.000$

  3. $99.999\approx 100.000$


Teste dein Wissen ... | DFU

Aufgabe 7 Das Urmeter

1889 einigte man sich auf der Generalkonferenz für Maß und Gewicht durch einen Meterprototypen aus einer Legierung aus 90 % Platin und 10 % Iridium. 1960 wurde diese Prototyp durch die Messung einer Wellenlänge ersetzt. Trotz allem gibt es bis heute verschiedene Längeneinheiten. Gib die folgenden Längen in Meter an.

  1. 1 Zoll

  2. 1 Meile

  3. 1 Fuß

  4. 1 Seemeile

  5. Übersetze die Angaben für Zoll, Fuß und Meile in die englische Sprache.

Maßstab

  1. 1 Zoll = 1,54 cm

  2. 1 Meile = 1,6 km

  3. 1 Fuß = 30,48 cm

  4. 1 Seemeile = 1,852 km

  5. Zoll - inch, Meile - mile, Fuß - foot



Entspann dich erst mal ...

Das Universum

Unser Universum ist unvorstellbar groß und doch endlich. Einen guten Überblick über dessen Größe gibt dieses Video.

Aufgabe 8 Längen­angaben

Gib alle Längen jeweils in der größeren und kleineren Einheit an.

  1. $270$ cm
  2. $280$ dm
  3. $4700$ m
  1. $560$ cm
  2. $27000$ m
  3. $2700$ cm
  1. $680$ m
  2. $7500$ m
  3. $27000$ m
  1. $2700$ mm $=270$ cm $=27$ dm
  2. $2800$ cm $=280$ dm $=28$ m
  3. $47000$ dm $=4700$ m $=4,7$ km
  1. $5600$ mm $=560$ cm $=56$ dm
  2. $270.000$ dm $=27000$ m $=27$ km
  3. $270.000$ dm $=2700$ cm $=270$ dm
  1. $6800$ dm $=680$ m $=0,68$ km
  2. $75.000$ dm $=7500$ m $=7,5$ km
  3. $270.000$ dm $=27000$ m $=27$ km


Aufgabe 9 Zeitangaben

Gib die Zeitangaben in 2 Maßeinheiten an.

  1. $64\:\text{s}$
  2. $91\:\text{s}$
  3. $140\:\text{s}$
  1. $75\:\text{min}$
  2. $100\:\text{min}$
  3. $200\:\text{min}$
  1. $29\:\text{h}$
  2. $57\:\text{h}$
  3. $240\:\text{h}$
  1. $63\:\text{h}$
  2. $84\:\text{min}$
  3. $500\:\text{s}$
  1. $64\:\text{s}=1\:\text{min}+4\:\text{s}$
  2. $91\:\text{s}=1\:\text{min}+31\:\text{s}$
  3. $140\:\text{s}=2\:\text{min}+20\:\text{s}$
  1. $75\:\text{min}=1\:\text{h}+15\:\text{min}$
  2. $100\:\text{min}=1\:\text{h}=40\:\text{min}$
  3. $200\:\text{min}=3\:\text{h}=20\:\text{min}$
  1. $29\:\text{h}=1\:\text{d}+5\:\text{h}$
  2. $57\:\text{h}=2\:\text{d}+9\:\text{h}$
  3. $240\:\text{h}=10\:\text{d}$
  1. $63\:\text{h}=2\:\text{d}+15\:\text{h}$
  2. $84\:\text{min}=1\:\text{h}+24\:\text{min}$
  3. $500\:\text{s}=8\:\text{min}+20\:\text{s}$

Aufgabe 10 Zeitangaben

Marienkirche München

Finde die richtige Uhrzeit heraus.

  1. Es ist 7.50 Uhr. Die erste Schulstunde dauert 45 min. Wann ist Pause?
  2. Es ist 20 Uhr. Vor 90 min sind sie losgelaufen. Wann sind sie gestartet?
  3. Es ist 18.30 Uhr. Vor 4 Stunden sind sie gestartet. Normalerweise benötigen sie für die Strecke 7 Stunden. Wann werden sie ankommen?

  1. Pause ist um 8.35 Uhr.
  2. Sie sind um 18.30 Uhr gestartet.
  1. Sie kommen voraussichtlich um 21.30 Uhr an.

Aufgabe 11 Gewichtsangaben

  1. Ordne der Größe nach:
    12 kg - 401 g - 1,4 kg - 0,002 kg - 100 kg - 1,5 kg - 700 kg.
  2. Runde auf volle kg:
    2222 g, 670 g, 115.624 g, 3712 g, 5.555 g.
  3. Schreibe in einer anderen Gewichtseinheit:
    100 g Käse enthalten:
    Eiweiß 10,3 g - Fett 7,2 g - Natrium 0,001 g - Vitamin C 60 g - Eisen 4 mg - Magnesium 151 mg
Gewichte

  1. Der Größe nach geordnet:
    700 kg - 100 kg - 12 kg - 1,5 kg - 1,4 kg - 401 g - 0,002 kg.
  2. Auf volle kg gerundet:
    2222 g $\approx$ 2 kg,
    670 g $\approx$ 1 kg,
    115.624 g $\approx$ 116 kg,
    3712 g $\approx$ 4 kg, 5.555 g $\approx$ 6 kg
  1. Angaben in anderer Gewichtseinheit:
    0,1 kg Käse enthalten:
    Eiweiß 0,0103 kg - Fett 0,0072 kg - Natrium 1 mg - Vitamin C 0,06 kg - Eisen 0,004 g - Magnesium 0,151 g

Wortliste und Satzbausteine



1 Tausend $1\:000$ hat 3 Nullen
1 Million $1\:000\:000$ hat 6 Nullen
1 Milliarde $1\:000\:000\:000$ hat 9 Nullen
1 Billion $1\:000\:000\:000\:000$ hat 12 Nullen
runden, man rundet $17 \approx 20$ und $13 \approx 10$
$\approx$ ist ungefähr gleich
auf­runden, man rundet auf $16 \approx 20$. Wenn man 16 auf Zehner rundet, dann rundet man auf.
ab­runden, man rundet ab $124 \approx 100$. Wenn man 124 auf Hundert rundet, dann rundet man ab.
$<$ ist kleiner als
$>$ ist größer als
$=$ ist gleich
die Größe, -en Als physikalische Größen bezeichnet man die Länge, das Gewicht und die Zeit.
die Einheit, -en Größen wie die Länge, das Gewicht und Zeit haben Einheiten. Die Länge wird in der Einheit Meter (m), das Gewicht in Kilogramm (kg) und die Zeit in Sekunden (s) gemessen.
die Länge, -n Die Länge ist ein Maß für die Strecke entlang eines Weges. Die Länge wird in Meter (m) gemessen.
$$1\:\text{km}=1.000\:\text{m}=1.000.000\:\text{mm}$$
das Ge­wicht, -e Das Gewicht ist ein Maß für die Kraft, welche auf einen Körper aufgrund der Erdanziehung wirkt. Das Gewicht wird in Kilogramm (kg) angegeben. $$1\:\text{kg}=1.000\:\text{g}=1.000.000\:\text{mg}$$
die Zeit, -en Die Zeit ist ein Maß für die Abfolge von Ereignissen. Die Zeit wird in Stunden (h), Minuten (min) und Sekunden (s) gemessen. $$1\:\text{h}=60\:\text{min}=3.600\:\text{s}$$
stoppen, er/sie stoppt Bei einem 1000 m-Lauf stoppt man die Zeit.
messen, er/sie misst Man misst eine Länge von 22 m.
wiegen, er/sie wiegt Jan wiegt 4 kg Obst.
die Stoppuhr, -en Die Stoppuhr benötigst du, um die Zeit stoppen.
das Maßband, -"er Das Maßband benötigst du, um die Länge zu messen.
die Waage, -en Die Waage benötigst du, um das Gewicht zu bestimmen.
© mylime.info