Reihen- und Parallelschaltung

Ideen:
J. Schwarz Elektronikschule Tettnang, 2006

In einem Stromkreis befinden sich oft mehrere Verbraucher. Sie werden entweder in Reihe hintereinander oder parallel geschaltet.

Hier wird die Funktionsweise der Reihen- und Parallelschaltung in der Elektrotechnik erklärt. Begriffe wie Gesamtspannung, Gesamtwiderstand und Gesamtstrom sowie Verhältnisse aus Widerstand, Spannung und Strom werden erklärt.

Die Reihenschaltung und Parallelschaltung

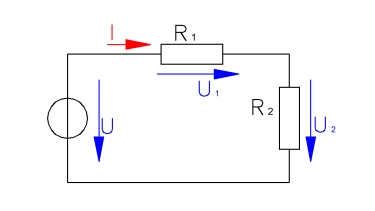
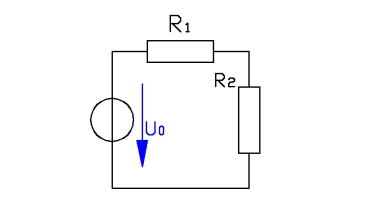
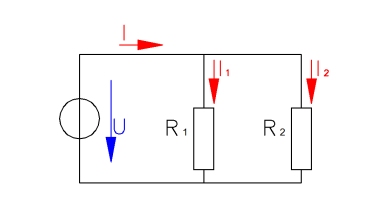
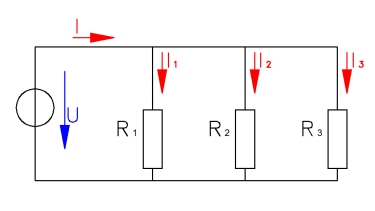
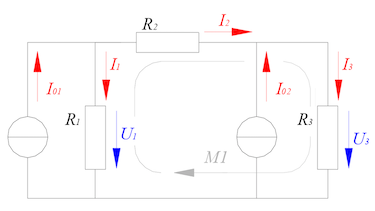
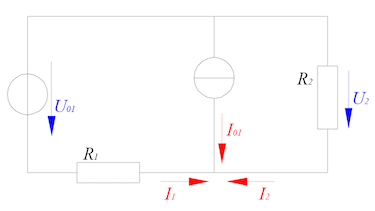
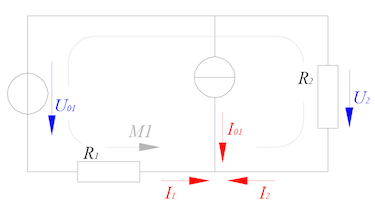
In der Reihenschaltung werden die Verbraucher in Reihe hintereinander geschaltet, wie bei einer Lichterkette. Fällt ein Verbraucher aus, fließt durch keinen mehr Strom. In der Parallelschaltung hingegen, werden die Verbraucher nebeneinander angeschlossen. Fällt hier ein Verbraucher aus funktionieren die anderen noch.

Nun könnte man ja meinen, dass in diesem Fall die Reihenschaltung gar kein Sinn mehr macht. Dem ist aber nicht so. In diesem kurzen Tutorial erfahrt ihr wieso. Ausserdem werden die verschiedenen mathematischen Zusammenhänge zwischen den elektrischen Größen erklärt.

Die Reihenschaltung

Der deutsche Physiker Gustav Kirchhoff untersuchte die Schaltung genauer und fand heraus, dass der Strom in der gesamten Schaltung konstant ist,

$$I=konstant$$

die Gesamtspannung ist die Summe der Teilspannungen,

$$U=U_1+U_2$$

der Gesamtwiderstand ist die Summe der Einzelwiderstände.

$$R=R_1+R_2$$

So lassen sich, bei geringen Materialverbrauch, Leuchtmittel hintereinander schalten.

Die Maschenregel - Kirchhoff 2

Er verallgemeinerte das Summengesetz der Spannungen zur Maschenregel:
Die Summe aller Spannungen in einer Masche ist gleich Null. $$\Sigma U=0$$

Weiter stellte er einen wichtigen Zusammenhang zwischen Widerständen und Spannungen her:
Die Widerstände verhalten sich wie die Spannungen. $$\frac{R_1}{R_2}=\frac{U_1}{U_2},~\frac{R}{R_1}=\frac{U}{U_1}$$

Aufgabe 1 Reihenschaltung

Eine Lichterkette aus 24 in Reihe geschalteten Leuchtmitteln gleicher Leistung liegt an einer Spannung von 230 V.

Welche Spannung liegt an jedem Leuchtmittel?

Für 4 durchgebrannte Leuchtmittel werden Drahtbrücken eingelegt.

Um wie viel % erhöht sich die Spannung an jedem Leuchtmittel?
Wie hoch ist der Spannungsfall an einem durchgebrannten Leuchtmittel ohne Drahtbrücke?
Bewerte: Ist es gefährlich eine Drahtbrücke unter Spannung einzusetzen?

$U_1=9,58~V$
$U_1=11,5~V,~~~20,04~\%$
$U_1=230~V$

Aufgabe 2

Zwei Widerstände sind in Reihe an U₀ = 24 V geschaltet. Es fließt ein Strom von 120 mA. Berechne

den Gesamtwiderstand R,
den Widerstand R₁, wenn der Spannungsfall hier 7 V betragen soll.

$R=\frac{U}{I}=\frac{24~V}{120~mA}=200~\Omega$
$R_1=R\cdot\frac{U_1}{U}=58,33~\Omega$

Die Parallelschaltung

Gustav Kirchhoff, der übrigens 1824 geboren wurde, untersuchte auch die Parallelschaltung. Hier zeigte er, dass die Spannung in der gesamten Schaltung konstant ist,

$$U=konstant$$

der Gesamtstrom in einem Punkt sich aus der Summe der Teilströme zusammensetzt,

$$I=I_1+I_2$$

und der Gesamtwiderstand sich über dessen Kehrwert bestimmen lässt.

$$\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}$$

Parallelschaltung von zwei Widereständen

Knotenregel - Kirchhoff 1

Er verallgemeinerte das Summengesetz der Ströme zur Knotenregel:
Die Summe aller Ströme in einem Knoten ist gleich Null.

$$\Sigma I=0$$

Auch hier stellte er einen wichtigen Zusammenhang zwischen Widerständen und Strömen her:
Die Widerstände verhalten sich umgekehrt wie die Ströme.

$$\frac{R_1}{R_2}=\frac{I_2}{I_1},~\frac{R}{R_1}=\frac{I_1}{I}$$

Aufgabe 3 Parallelschaltung

Drei Widerstände R₁ = 10 kΩ, R₂ = 7 kΩ und R₃ = 15 kΩ sind parallel geschaltet. Der Strom beträgt I = 3,71 mA.

Berechne den Ersatzwiderstand der Schaltung.
Wie groß sind die Teilströme I₁, I₂ und I₃? Rechne über das Verhältnis.
Berechne den Gesamtstrom I, wenn R₃ ausfällt?

$R=\frac{1}{\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}}=3230,77~\Omega$
$I_1=I\cdot\frac{R}{R_1}=1,20~mA$

$I_2=I\cdot\frac{R}{R_2}=1,71~mA$

$I_3=I\cdot\frac{R}{R_3}=0,798~mA$
$I=I_1+I_2=2,91~mA$

Aufgabe 4 Gemischte Schaltung

Durch die gemischte Schaltung fließt der Strom I₂ = 75 mA und I₃ = 25 mA. Der Widerstand R₁ beträgt 2,2 kΩ, R₂ beträgt 1 kΩ.

Berechne R₃.
Berechne den Ersatzwiderstand.
Wie groß ist die Spannung U?

Lösungshinweise:

$\frac{R_3}{R_2}=\frac{I_2}{I_3}$
$R=R_1+\frac{1}{\frac{1}{R_2}+\frac{1}{R_3}}$
$U=R\cdot (I_2+I_3)$

Aufgabe 5 Welche Aussage ist wahr?

Wähle die korrekten Aussagen zur gegebenen Schaltung aus.

Nenne die beiden Widerstände, die zuerst zusammengefasst werden.
Wähle eine Antwort.

$R_2$ und $R_3$
$R_3$ und $R_4$
$R_1$ und $R_2$
$R_4$ und $R_5$

Berechne den Ersatzwiderstand $R_{123}$.
Wähle eine Antwort.

$0,5\:\text{k}\Omega$
$1\:\text{k}\Omega$
$2\:\text{k}\Omega$
$4\:\text{k}\Omega$

Berechne den Ersatzwiderstand $R_{1234}$.
Wähle eine Antwort.

$0,5\:\text{k}\Omega$
$1\:\text{k}\Omega$
$2\:\text{k}\Omega$
$4\:\text{k}\Omega$

Berechne den Ersatzwiderstand $R_{12345}$.
Wähle eine Antwort.

$0,5\:\text{k}\Omega$
$1\:\text{k}\Omega$
$2\:\text{k}\Omega$
$4\:\text{k}\Omega$

Berechne den Ersatzwiderstand $R_{1234567}$.
Wähle eine Antwort.

$0,5\:\text{k}\Omega$
$1\:\text{k}\Omega$
$2\:\text{k}\Omega$
$4\:\text{k}\Omega$

Die Schaltung wird auf 99 Widerstände erweitert. Berechne den Ersatzwiderstand $R_{1...99}$.
Wähle eine Antwort.

$0,5\:\text{k}\Omega$
$1\:\text{k}\Omega$
$2\:\text{k}\Omega$
$4\:\text{k}\Omega$

Maschenstromverfahren

Gegeben ist $I_{01}=10\:mA$, $I_{02}=7\:mA$, $R_1=R_2=R_3=1\:k\Omega$.
Gesucht ist $I_3$.

1. Wähle die Masche ohne Stromquellen
$R_2I_2+R_3I_3=R_1I_1$

2. Nicht gesuchte Ströme ersetzen
$I_2=I_3-I_{02}$ und $I_1=I_{01}-I_2=I_{01}-I_3+I_{02}$
$R_2(I_3-I_{02}+R_3I_3=R_1(I_{01}-I_3+I_{02})$

3. Gleichung nach gesuchter Größe (hier $I_3$) umstellen
$R_2(I_3-I_{02})+R_3I_3=R_1(I_{01}-I_3+I_{02})$
$R_2I_3-R_2I_{02}+R_3I_3=R_1I_{01}-R_1I_3+R_1I_{02}$
$R_2I_3+R_3I_3+R_1I_3=R_1I_{01}+R_1I_{02}+R_2I_{02}$
$I_3(R_2+R_3+R_1)=R_1I_{01}+R_1I_{02}+R_2I_{02}$

$$I_3=\frac{R_1I_{01}+R_1I_{02}+R_2I_{02}}{R_2+R_3+R_1}=8\:mA$$

Maschenstromverfahren nach Gauß

Gegeben ist $I_{01}=3\:A$, $I_{02}=5\:A$, $R_1=2\:\Omega$, $R_2=1\:\Omega$, $R_3=4\:\Omega$.
Gesucht ist $I_1$, $I_2$, $I_3$.

1. Wähle die Masche ohne Stromquellen und die Knoten. Pro unbekannter Größe benötigt man eine Gleichung
$\left| \begin{array}{ccccc} -R_1I_1 & +R_2I_2 & +R_3I_3 &=&0 \\ 0 & +I_2 & -3 &=&-I_{02} \\ I_1 & +I_2 & +0 &=&I_{01} \\ \end{array} \right|$

2. Gleichungssystem nach Gauß bis zur Dreiecksform umstellen
$\left| \begin{array}{ccccc} -2I_1 & +I_2 & +4I_3 &=&0 \\ 0 & +I_2 & -I_3 &=&-5 \\ I_1 & +I_2 & +0 &=&3 \\ \end{array} \right| \begin{array}{c} \\ \\ \cdot 2+I\\ \end{array} \\$

$\left| \begin{array}{ccccc} -2I_1 & +I_2 & +4I_3 &=&0 \\ 0 & +I_2 & -I_3 &=&-5 \\ 0 & +3I_2 & +4I_3 &=&6 \\ \end{array} \right| \begin{array}{c} \\ \\ +(-3)\cdot II \\ \end{array} \\$

$\left| \begin{array}{ccccc} -2I_1 & +I_2 & +4I_3 &=&0 \\ 0 & +I_2 & -I_3 &=&-5 \\ 0 & 0 & +7I_3 &=&21 \\ \end{array} \right| \begin{array}{c} \\ \\ +(-3)\cdot II \\ \end{array} \\$

3. Durch Einsetzen lösen
$I_3=3\:$A,
$I_2=-2\:$A,
$I_1=5\:$A

Aufgabe 6 Maschenstromverfahren

Mit dem Maschenstromverfahren ist der Strom und die Spannung am Widerstand R₂ zu bestimmen.

Folgende Werte sind bekannt:
R₁ = 120 Ω, R₂ = 470 Ω, I₀₁ = 12 mA und U₀₁ = 24 V.

Masche über beide Widerstände und Spannungsquelle:

$U_{01}+U_1-U_2=0$

$U_{01}+R_1I_1-R_2I_2=0~~~~|I_1=-I_{01}-I_2$

$U_{01}-R_1I_{01}-R_1I_2-R_2I_2=0$

$I_2(-R_1-R_2)=R_1I_{01}-U_{01}$

$I_2=\frac{R_1I_{01}-U_{01}}{(-R_1-R_2)}$

$I_2=38,24~mA$

$U_2=R_2I_2=17,97~V$

Aufgabe 7 Welche Aussage ist wahr?

Wähle die korrekten Aussagen zur gegebenen Schaltung aus.

In der folgenden Schaltung sind $U_{01}=10\:V$, $I_{01}=10\:mA$, $R_1=R_2=1\:k\Omega$. Gesucht ist der Strom $I_2$.

Stelle die korrekte Masche auf.
Wähle eine Antwort.

$I_1R_1+I_2R_2=U_{01}$
$I_2R_2+I_1R_1=0$
$I_2R_2+I_1R_1+I_3R_3$=0
$I_2+I_3=R_1$

Gib den korrekten Knoten an.
Wähle eine Antwort.

$I_1=I_2+I_{01}$
$I_2=I_1+I_{01}$
$I_{01}=I_2-I_1$
$I_1-I_2=-I_{01}$

Gib die zweite Zeile der Dreiecksform nach Gauß an.
Wähle eine Antwort.

$1000I_2=7$
$0+2000I_2=20$
$1000I_1+1000I_2=10$
$0+1000I_2=20$

Berechne $I_2$
Wähle eine Antwort.

$6\:mA$
$10\:mA$
$14\:mA$
$22\:mA$