immer steiler werdende Bergwiese

Einführung in die Differenzialrechnung

Die Differenzialrechnung beschäftigt sich mit den Eigenschaften mathematischer Funktionen. Dazu gehören die soge­nann­ten Ableitungen, die uns die Stei­gung einer Funktion angeben. Wie und warum das funktioniert, wird in diesem Artikel erklärt.

1 Die immer steilere Bergwiese



Mutterschaf mit Lämmern auf einer Bergwiese

Eine traumhafte Bergwiese in 2000 m Höhe. Doch Vorsicht! Sie wird immer steiler und steiler. Ab welcher Steigung wird es gefährlich? Müsste ich dafür nicht die Steigung erst einmal kennen? Und als Mathematiker stelle ich mir natürlich die Frage: "Wie kann ich die Steigung in einer Funktion die ständig ihren Wert ändert überhaupt bestimmen?

Mit diesen Fragen beschäftigt sich die Differentialrechnung. Sie hat eine Me­thode entwickelt mit der wir an belie­bi­ger Position die Steigung exakt bestim­men können. Neugierig? Wie das funk­tio­niert, wirst Du in diesem Artikel lernen.

2 Vermessen



gespannte Schnur

Die Parabel ändert ständig ihre Steigung.

$$f(x)=x^2$$

Zeichne eine Parabel auf den Schulhof. Am besten zeichnest du zur besseren Orien­tierung gleich noch die Achsen mit. Nun stellt sich einer von euch an einen beliebigen Punkt A, von dem er die Steigung wissen möchte. Spanne eine Schnur zu einem weiteren Punkt B auf der Parabel und bestimme die Steigung dieser Geraden. Wie müsstest du den Punkt B verschieben, damit die Steigung exakter zu Punkt A passt?

|enaktiv

3 Testen der Werte



verlegte Randsteine

Nun wollen wir die Steigungen ermitteln. Zeichne hierzu die Steigungsgerade zwi­schen Punkt A und Punkt B in die Pa­ra­bel ein. Dann halbiere den Abstand und zeichne erneut eine Steigungsgerade ein. Schaffst du es den Abstand nochmal zu halbieren und eine weitere Steigungsgerade einzuzeichnen?

Lässt sich mit dieser Methode die Stei­gung in Punkt A herausfinden? Wie nah müsstest du an den Punkt A heran­rücken und wie groß ist die Steigung?

|ikonisch+numerisch

4 Steigung der Tangente



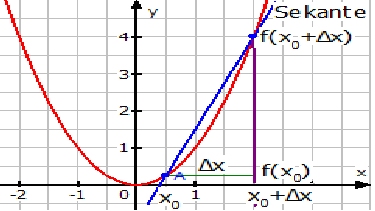
Parabel

Für die Steigung der Sekante gilt:

$$m_S=\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$$

Für die Steigung der Tangente gilt:

$$=\lim_{\Delta x \to 0} 2x_0+\Delta x=2x_0$$

|symbolisch

5 Ableitung einer Funktion



slopestyle

Die Steigung einer Funktion f wird als Ableitung f’ bezeichnet. Da sich die Steigung in jedem Punkt ändert ist f' wiederum eine Funktion.

$$f(x) = x^2 ~~~~ f'(x)=m_T=2x$$

Die Steigung der Tangente, man könnt auch sagen: "Die Steigung der Steigung" hat den konstanten Wert 2. Man spricht von der 2. Ableitung f''.

$$f''(x)=f'(f(x))=2$$

6 Ableitung höherer Ordnung



slopestyle in Aktion

Beim Springen werden Kurven höhere Ordnung durchfahren, wie bspw. $f(x)=x^3$. Welche Steigungen durchläuft ein Skispringer?

$f'(x) = \lim_{\Delta x \to 0} \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} $$= \lim_{\Delta x \to 0} \frac{(x_0+\Delta x)^3-x_0^3}{\Delta x}$ $= \lim_{\Delta x \to 0} \frac{\Delta x(3x_0^2+3x_0\Delta x+\Delta x^2)}{\Delta x}$$=3x_0^2$

Potenzregel:

$$f(x)=x^n~\Rightarrow~f'(x)=nx^{n-1}$$

7 Faktorregel und Summenregel



Ableitung der Funktion $f(x)=5x^2$:

$f'(x) = \lim_{\Delta x \to 0} \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} $ $= \lim_{\Delta x \to 0}\frac{5(x_0+\Delta x)^2-5x_0^2}{\Delta x} $ $= \lim_{\Delta x \to 0}2\cdot 5 x_0 + 5\Delta x $ $=2\cdot 5 x_0$

Faktorregel: Konstante Faktoren bleiben erhalten.

$$f(x)=ax^2 \Rightarrow~f'(x)=2ax$$

Ableitung von $f(x)=5x^2+4x+3$:

$f'(x) = \lim_{\Delta x \to 0} \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} $ $= \lim_{\Delta x \to 0}\frac{5(x_0+\Delta x)^2+4(x_0+\Delta x)+3-...}{\Delta x} $ $= \lim_{\Delta x \to 0}2\cdot 5 x_0 + 5\Delta x +4 $ $=2\cdot 5 x_0+4$

Summenregel: Jeder Summand wird einzeln abgeleitet.

$$f(x)\hspace{-0.5mm}=\hspace{-0.5mm}ax^2\hspace{-1mm}+\hspace{-0.5mm}bx~\Rightarrow~\hspace{-0.5mm}f'(x)\hspace{-0.5mm}=\hspace{-0.5mm}2ax\hspace{-0.5mm}+\hspace{-0.5mm}b$$

Aufgabe 1 Faktorregel und Summenregel

Berechne die erste Ableitung $f'(x)$

  1. $f(x)=1/3x^2$
  2. $f(x)=-4x^2$
  3. $f(x)=x^2-4x+3$
  1. $f(x)=-3/2x^2+3/4x$
  2. $f(x)=-3x+2$
  1. $f'(x)=2/3x$
  2. $f'(x)=-8x$
  3. $f'(x)=2x-4$
  1. $f'(x)=-3x+3/4$
  2. $f'(x)=-3$

Entspann dich erst mal ...

Zwei Mathematiker und zwei Physiker fahren zusammen mit der Bahn zu einem Kongress. Auf der Hinfahrt unterhalten sie sich über die Systematik des Fahrkartenverkaufs, wobei die Mathematiker erwähnen, dass sie nur eine Fahrkarte für zwei Personen brauchen. Als nach einiger Zeit sich der Schaffner nähert, gehen die beiden Mathematiker zusammen aufs Klo (auf dasselbe!). Kurz darauf klopft der Schaffner an die Tür und verlangt die Fahrkarte, die Mathematiker schieben ihre unter der Tür durch, und alles ist okay.

Auf der Rückfahrt haben die Physiker dazugelernt und auch nur eine Fahrkarte gekauft. Die Mathematiker haben dagegen gar keine! Wiederum nähert sich bald der Schaffner, und die Physiker begeben sich aufs Klo. Kurz darauf geht ihnen ein Mathematiker nach und klopft an die Tür: "Die Fahrkarte bitte!"

Was lernen wir daraus? Die Physiker wenden mathematische Verfahren an, ohne sie wirklich zu verstehen.

Quelle: uwenowak.de/humor/mathewitze.xhtml

Aufgabe 2 Potenz- und Summenregel

Bilde jeweils die erste und zweite Ableitung.

  1. $f(x)=x^3-4$
  2. $f(x)=-3/2x^4+3/4x$
  3. $f(x)=2$
  1. $f(x)=-\frac{1}{8}(x^2-4x)$
  2. $f(x)=(x-2)x^2$
  3. $f(x)=1/12x^4+1/2x^2$
  1. $f'(x)=3x~~~~~~f''(x)=3$
  2. $f'(x)=-6x^3+3/4~~~~~~f''(x)=-18x^2$
  3. $f'(x)=0~~~~~~f''(x)=0$
  1. $f'(x)=-\frac{1}{8}(2x-4)~~~~~~f''(x)=-\frac{2}{8}$
  2. $f'(x)=3x^2-4x~~~~~~f''(x)=6x-4$
  3. $f'(x)=1/3x^3+x~~~~~~f''(x)=x^2+1$

Aufgabe 3 Die Parabel und die Schafe

Schafe am Hang

Schafe können an Hängen mit einer Neigung von bis zu 45 ° grasen. An welcher x-Position hat die Parabel $f(x)=-x^2$ eine Steigung von 45 °?

Hinweis: Rechne hierfür die Winkelangabe in eine %-Steigungsangabe um.

Umrechnung der Winkelangabe: $m=tan 45^{\circ}=1$

Ableiten:
$f(x)=-x^2$
$f'(x)=-2x$
$f'(x)=1~\Rightarrow~x=-0,5$

Aufgabe 4 Die Parabel, Idee: J. Blum

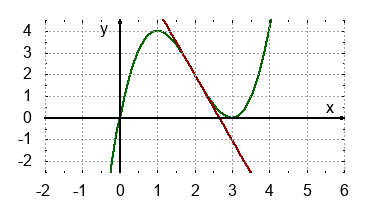
Dargestellt ist die Funktion $f(x) = x^2-6x+9$.

  1. Zeichne das Schaubild der Ableitungsfunktion $f'(x)$
  2. Skizziere in einer anderen Farbe den Graph, zu dem $f$ selber die Ableitung ist.
  3. Ermittle zeichnerisch die Steigung der Tangenten an der Stelle $x_0=3,5$.
  4. Berechne die Steigung an der Stelle $x_0=3,5$ mit Hilfe des Diffenezenquotienten.
  5. Betimme die Gleichung der Tangenten an der Stelle $x_0=3,5$.
Schaubild der Funktion f(x)=x^2-6x+9

  1. Schaubild der Ableitungsfunktion $f'(x)$:
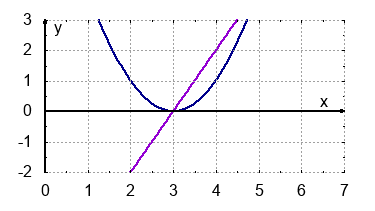
    Schaubild der Funktion f(x)=x^2-6x+9
  2. Graph, zu dem $f$ selber die Ableitung ist:
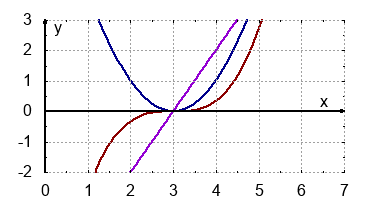
    Schaubild der Funktion f(x)=1/3x^3-6/2x^2+9x-9
  1. Ermittle zeichnerische die Steigung der Tangenten an der Stelle $x_0=3,5$:
    Schaubild der Tangenten an der Stelle x0
  2. Steigung an der Stelle $x_0=3,5$: $m=1$
  3. Gleichung der Tangenten an der Stelle $x_0=3,5$: $f(x)=x-3,25$

Aufgabe 5 Idee J. Blum, CDSC

Gegeben sind $f(x) = -x^2+4$ und $g(x)=x^2-5x+6$.

Schaubild der Funktion f(x)=x^2-6x+9

  1. Bestimme die Ableitungsfunktionen $f'(x)$ und $g'(x)$.
  2. An welcher Stelle $x_1$ haben $f$ und $g$ die identische Steigung?
  3. An welcher Stelle $x_2$ ist die Steigung der Tangente an f(x) parallel zur Geraden $y=4x-3$?
  4. Betimme die Gleichung der Tangenten von f an der Stelle $x_3=-1,5$.
  1. $f'(x)=-2x$, $g'(x)=2x-5$
  2. $x_1=1,25$
  3. $f'(x)=4$: $x_2=-2$
    Schaubild der Funktion f(x)=1/3x^3-6/2x^2+9x-9
  1. $y=3x+6,25$

Aufgabe 6 Parable 2. und 3. Ordnung

Gegeben sind $f(x) = x^3-6x^2+9x$ und $g(x)=-(x-3)^2$.

  1. Bestimme die Ableitungsfunktionen $f'(x)$ und $g'(x)$.
  2. An welcher Stelle $x$ haben $f$ und $g$ die identische Steigung?
  3. Bestimme den Funktionsterm der Tangente von $f$ an der Stelle $x=2$.
  4. Betimme die Gleichung der Tangenten von f an der Stelle $x=4$.
  5. Bestimme den Funktionsterm der Orthogonale von $f$ an der Stelle $x=2$.
  6. An welcher Stelle $x$ ist die Steigung von f(x) parallel zur Geraden $y=0$?
  7. Bestimme die Nullstellen von f.
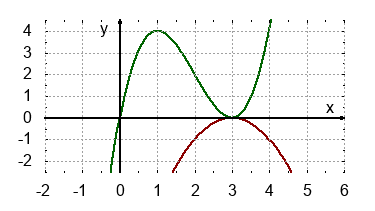
Schaubild eine Parabel 2. und 3. Ordnung

  1. $f'(x)=3x^2-12x+9$, $g'(x)=-2x+6$
  2. Gleichsetzten der Ableitungsgleichungen:
    $\begin{equation*} \begin{array}{cc} f'(x) &=& g'(x)\\ 3x^2-12x+9 &=& -2x+6 |+2x-6\\ 3x^2-10x+3 &=& 0 |:3\\ x^2-10/3x+1 &=& 0 |-1+(5/3)^2\\ (x-5/3)^2 &=& 25/9-9/9 |\sqrt{..}\\ (x-5/3) &=& \pm 4/3 |+5/3 \\ x_1=1/3 &|& x_2=3\\ \end{array} \end{equation*} $
  3. $y=-3x+8$
    Schaubild einer Funktion und Tangente
  4. Tangente: y=9x-32
  1. $m_O=-1/m_T=-1/3$
    Somit ist $y=-1/3x+5/3$
    Schaubild einer Funktion und Orthogonale
  2. Ableitung gleich Null setzen:
    $\begin{equation*} \begin{array}{cc} f'(x) &=& 0\\ 3x^2-12x+9 &=& 0 |:3\\ x^2-4x+3 &=& 0 |-3+2^2\\ (x-2)^2 &=& 1 |\sqrt{..}\\ (x-2) &=& \pm 1 |+2 \\ x_1=1 &|& x_2=3\\ \end{array} \end{equation*} $
  3. Nullstellen: $x_1=0$, $x_2=3$

Aufgabe 7 Wachstum einer Kiefer

Das Wachstum einer Kiefer kann in den ersten 30 Jahren nach Pflanzung mit folgender Funktion beschrieben werden: $W(t) = -0.005t^3+0.2t^2+0.9t+1$. Dabei gibt $W(t)$ die Höhe in m an.

Kiefer

  1. Berechne die Höhe nach 21 Jahren.
  2. Bestimme die durchschnittliche Wachstumsgeschwindigkeit in 21 Jahren.
  3. Bestimme die Wachstumsgeschwindigkeit zur Beginn.
  4. Wann ist die Wachstumsgeschwindigkeit genau so groß wie zu Beginn? Bestimme die Jahre und Monate.
  1. 62 m
  2. 2,9 m/Jahr
  3. 0,9 m/Jahr
  1. 26 Jahre und 8 Monate