Eine Menge Ananas

Zahlen­mengen und Terme

Hier erfährst du alles über die verschiedenen Zahlenmengen, den Betrag und das Rechnen mit Termen

1 Zahlenmengen
Zahlenmengen

In der Mathematik werden folgende Zahlenmengen definiert:

  1. Natürliche Zahlen $\mathbb{N}$: 0, 1, 2, 3 ...
  2. Ganze Zahlen $\mathbb{Z}$: ... -3, -2, -1, 0, 1 ...
  3. Rationale Zahlen $\mathbb{Q}$: ... $-3$, $-2.5$, $-1$, $-1/2$, 0, $0,\bar{3}$, $1\frac{1}{2}$ ...
  4. Reele Zahlen $\mathbb{R}$: $\pi$, $-\pi$, $e$, $\sqrt{2}$, $2$, $-0,3$ ...
2 Der Betrag
Porsche

Der Betrag der Geschwindigkeit ist das Tempo. Während jede Geschwindigkeit eine Richtung hat, ist das Tempo richtungsunab­hängig.

Der Betrag einer Zahl gibt deren Wert ohne Vorzeichen an. Man schreibt:

$$|-7|=7 \quad \quad |+3|=3$$
3 Änderungen
Gänse

Bauer Jan hatte im letzen Jahr 4 Gänse, dieses Jahr sind es 12. Um wie viele Gänse ist sein Bestand gewachsen?

$$4 \quad \underrightarrow{+8} \quad 12$$

Solche Fragen geben eine Antwort auf die Änderung und diese ist in der Wissenschaft oft von größerer Bedeutung als der absolute Wert. Die zurück­ge­legte "Distanz" wird mit dem griechischen Buschtaben $\Delta$ abgekürzt. Man schreibt:

$$\Delta \text{Bestand} = 8$$
4 Summe der natürlichen Zahlen
$$\begin{equation*} \begin{array}{ccccc} & 1 & + & 100 & = & 101\\ & 2 & + & 99 & = & 101\\ & 2 & + & 99 & = & 101\\ & & & ... & & \\ & 50 & + & 51 & = & 101\\ \end{array} \end{equation*} $$

Möchtest du mal eine ganz schwierige Formel kennen lernen? Dann pass jetzt gut auf.

Bilde die Summe aller natürlichen Zahelen von 1 - 100.

$$1+ ... +100=50 \cdot 101 =5050$$

Allgemein gilt: Die Summe der natürlichen Zahlen von 1 bis n berechnet sich zu:

$$\sum_{k=1}^{n}k=\frac{n}{2} \cdot (n+1)$$
5 Variablen und Terme
$$1+3 \quad\quad y \quad\quad 4x : 2$$ $$\quad\quad x+3 \quad$$ $$x^2 \quad\quad\quad 4-2$$

Eine Variable ist ein Zeichen, dass für eine mögliche Zahl aus dem Zahlenbereich $\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$ oder $\mathbb{R}$ steht. Man schreibt für eine beliebige ganze Zahl:

$$x \in \mathbb{Z}$$

Ein Term ist ein mathematischer Ausdruck der aus Zahlen und Rechenzeichen ohne Gleich-/Ungleichzeichen besteht.

$$1+2+...+100 \quad \quad x-3$$

Ideen von P. Wunderlich, Seminar Weingarten



Aufgabe 1 Zahlenmenge

Menge von Zahlen

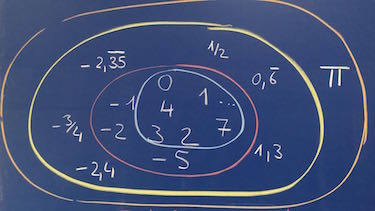
Zu welcher Zahlenmenge ($\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$, $\mathbb{R}$) gehören die abgebildeten Zahlen?

zugeordnete Zahlen


Aufgabe 2 Zahlenstrahl

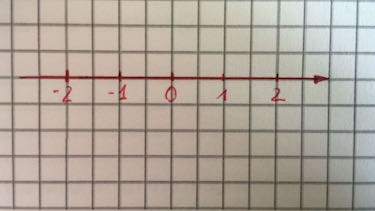
Ordne die folgenden Zahlen auf einem Zahlenstrahl an.

  1. 0   0,7   -3,4   4,1   -2,8   1,8
  2. 13   18   -8   -3   -25   -17
  3. -130   50   -20   220   -290
  4. $-2\frac{1}{10}$   $-0,4$   $\frac{1}{4}$   $2,5$   $3,75$   $4$
Zahlenstrahl

Zahlenstrahl


Aufgabe 3 Betrag

Zahl +12 0
Gegen­zahl -12 -3,4 17
Betrag 12 6

Vervollständige die Tabelle indem du Zahl, Gegenzahl und Betrag angibst.

Zahl +12 +3,4 +6 -17 0
Gegen­zahl -12 -3,4 -6 +17 0
Betrag 12 3,4 6 17 0


Entspann dich erst mal ...

Mal etwas lustiges.

... und los geht's

Wusstest du schon? "Eine ungerade Zahl mit einer ungeraden Zahl multipliziert, ergibt immer eine ungerade Zahl." Max aus Klasse 6, CDSC

Aufgabe 4 Änderung

Bestimme jeweils die Änderung oder den absoluten Wert.

  1. Der Aufzug fährt von OG 3 nach UG 2?

  2. Bei einem Tauchvorgang wurden folgende Tiefen notiert: -5 m, -12 m, -3 m, -10 m.

  3. Die Temperatur fällt von 3 °C auf -5 °C.

  4. Die Temperatur steigt von 18 °C auf 27°C.

  1. Julia fährt 3 Stockwerke nach unten und steigt in UG 1 aus.

  2. Nachdem es die letzten Tage 25 °C hatte, ist die Temperatur um 14 °C gefallen.

  3. Peter steigt im OG 4 aus und ist 7 Stockwerke nach oben gefahren.

  4. Nachdem das Konto 40 EUR im Minus war, habe ich 200 EUR eingezahlt.

  1. $\Delta \text{Ebene}=-(3-(-2))=-5$ Stockwerke

  2. $\Delta s=$ -7 m, +9 m, ...

  3. $\Delta T=-(3-(-5))=-8$ °C

  4. $\Delta T=27-18=+9$ °C

  1. OG 2

  2. 11 °C

  3. UG 2

  4. 160 EUR


Aufgabe 5 Wasserpegel

Stausee

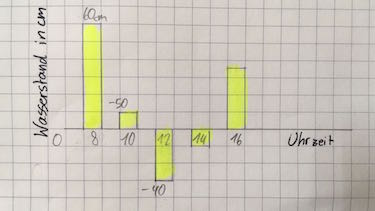
Der Level eines Bergbaches wird alle zwei Stunden gemessen. Um 8 Uhr beträgt der Wasserstand 60 cm über dem Normalstand. Um 10 Uhr ist der Wasserstand um 50 cm gefallen, um 12 Uhr um weitere 50 cm. Bis um 14 Uhr ist er wieder um 30 cm gestiegen und um 16 Uhr um weitere 40 cm.

Zeichne ein Uhrzeit-Wasserstandsdiagramm.

Uhrzeit-Waserstandsdiagramm


Quiz 1 Bankrutschen

Beim Schulbankrutschen, beginnt eine Schulbank mit Aufgabe 1. Wer das richtige Ergebnis sagt, rutscht eine Bank weiter. Wer die meisten Bänke gerutscht ist, ist Sieger.

  1. $-3-1=$
  2. $5+(-3)=$
  3. $-12-7=$
  4. $-3-(-3)=$
  5. $-3-(+3)=$
  1. $6\cdot(-3)=$
  2. $-4\cdot 3=$
  3. $-5\cdot (-7)=$
  4. $36 : (-6)=$
  5. $-3 \cdot (-3) : 2=$
  1. $-5 \cdot 12=$
  2. $-4-2\cdot 3=$
  3. $2\cdot 3 -4=$
  4. $-3-4\cdot(-2)=$
  5. $-12 -8 +10 =$
  1. $-3-1=-4$
  2. $5+(-3)=-8$
  3. $-12-7=-19$
  4. $-3-(-3)=0$
  5. $-3-(+3)=-6$
  1. $6\cdot(-3)=-18$
  2. $-4\cdot 3=-12$
  3. $-5\cdot (-7)=35$
  4. $36 : (-6)=-6$
  5. $-3 \cdot (-3) : 2=4,5$
  1. $-5 \cdot 12=-60$
  2. $-4-2\cdot 3=-10$
  3. $2\cdot 3 -4=2$
  4. $-3-4\cdot(-2)=5$
  5. $-12 -8 +10 =-10$

Aufgabe 6 Terme

Berechne.

  1. $-4 -5=$

  2. $-3 +7=$

  3. $+8 +(-12)=$

  4. $-5 - (-8)=$

  1. $11 - (-3)=$

  2. $-3 \cdot (-2)=$

  3. $-5 \cdot 12=$

  1. $-4 -5=-9$

  2. $-3 +7=4$

  3. $+8 +(-12)=-4$

  4. $-5 - (-8)=3$

  1. $11 - (-3)=14$

  2. $-3 \cdot (-2)=6$

  3. $-5 \cdot 12=-60$


Quiz 2 Die Matheschlange

Ihr tretet mannschaftsweise z.B. als Tischgruppen gegeneinander an. Der Schlangenkopf, der Schüler, der jeweils vorn steht muss rechnen. Derjenige Rechner, welcher zuerst das Ergenis sagt, stellt sich wieder hinten in seiner Reihe an. Wer zu langsam war, setzt sich an seinen Platz.

Die Schlange die als letztes stehende Mitspieler hat gewinnt.

Die Schülerinnen und Schüler die schon sitzen stellen die nächste Aufgabe und überprüfen das Ergebnis. So wird es niemandem langweilig.

  1. $-3-7+110=$
  2. $5,2-3=$
  3. $3-(4+2)=$
  4. $7-(3-1)=$
  1. $6\cdot(-3+2)=$
  2. $(-4-7)\cdot 3=$
  3. $-5\cdot (-7-13)=$
  4. $121 : (-11)=$
  1. $-5 \cdot 12:2=$
  2. $...$
  1. $-3-7+110=100$
  2. $5,2-3=3,2$
  3. $3-(4+2)=-3$
  4. $7-(3-1)=5$
  1. $6\cdot(-3+2)=-6$
  2. $(-4-7)\cdot 3=-33$
  3. $-5\cdot (-7-13)=100$
  4. $121 : (-11)=-11$
  1. $-5 \cdot 12:2=30$
  2. $...$


Aufgabe 7 Terme rationaler Zahlen

Berechne die Terme.

  1. $+\frac{7}{6} + \frac{3}{4} - \frac{2}{12} $
  2. $-\frac{1}{4} + \frac{2}{3} + \frac{10}{8} $
  3. $-\frac{3}{2} - \frac{7}{4} + \frac{12}{4} $
  4. $-\frac{1}{2} + \frac{2}{5} + (-\frac{6}{4})$
  5. $+\frac{3}{4} - 2 + 1,5 $
  1. $+3,25-4,6+0,75$
  2. $-7,4+2,6+3,5$
  3. $+6,8+15-1,8$
  4. $12,9+7,2+0,1$
  5. $-0,3-4,4-4,7$
  1. $+6,28 - 0,28 + 3,41$
  2. $+7,24 + 2,76 + 2,33$
  3. $+6,66 + 3,33 + 0,01$
  4. $-6,25 - 3,25 + 1,50$
  5. $-4,31 + 8,24 + 0,31$
  1. $-67,4 - 2,6 + 7,2 + 22,8$
  2. $ 27,2 + 9,2 - 7,2 + 10,8$
  3. $-33,2 + 3,5 - 7,5 - 2,8 $
  4. $ 15,7 + 6,7 + 4,3 + 13,3$
  5. $-12,9 - 1,1 - 5,1 - 20,9$
  1. $+\frac{7}{6} + \frac{3}{4} - \frac{2}{12} = \frac{7}{4}$
  2. $-\frac{1}{4} + \frac{2}{3} + \frac{10}{8} = \frac{5}{3}$
  3. $-\frac{3}{2} - \frac{7}{4} + \frac{12}{4} = -\frac{1}{4}$
  4. $-\frac{1}{2} + \frac{2}{5} + (-\frac{6}{4})= -\frac{8}{5}$
  5. $+\frac{3}{4} - 2 + 1,5 = \frac{1}{4}$
  1. $+3,25-4,6+0,75=-0,6$
  2. $-7,4+2,6+3,5=12,9$
  3. $+6,8+15-1,8=20$
  4. $12,9+7,2+0,1=20,2$
  5. $-0,3-4,4-4,7=9,4$
  1. $+6,28 - 0,28 + 3,41 = 9,41$
  2. $+7,24 + 2,76 + 2,33 = 12,33$
  3. $+6,66 + 3,33 + 0,01 = 10$
  4. $-6,25 - 3,25 + 1,50 = 2$
  5. $-4,31 + 8,24 + 0,31 = 4,24$
  1. $-67,4 - 2,6 + 7,2 + 22,8 =-40$
  2. $ 27,2 + 9,2 - 7,2 + 10,8 = 40$
  3. $-33,2 + 3,5 - 7,5 - 2,8 =-40$
  4. $ 15,7 + 6,7 + 4,3 + 13,3 = 40$
  5. $-12,9 - 1,1 - 5,1 - 20,9 =-40$


Aufgabe 8 Multiplitkation von Termen

Berechne die Terme.

  1. $\frac{3}{4} \cdot \frac{2}{3}$
  2. $\frac{4}{8} \cdot \left(-\frac{3}{7}\right)$
  3. $\frac{3}{9} \cdot \left(-6\right)$
  4. $\left(-\frac{7}{11}\right) \cdot \left(-\frac{121}{49}\right)$
  1. $0,36 \cdot \frac{10}{6}$
  2. $\left(-0,8\right) \cdot \left(\frac{7}{4}\right)$
  3. $\left(-2,25\right) \cdot \left(-\frac{3}{15}\right)$
  4. $\left(-0,\bar{3}\right) \cdot 3$
  1. $2,25 \cdot 4,1$
  2. $(-3,25) \cdot 6,3$
  3. $(-0,36) \cdot (-2,2)$
  4. $6,75 \cdot (-1,24)$
  1. $-\left((-3)-(-2) \right)$
  2. $-\left((-3)\cdot (-2) \right)$
  3. $-(2\cdot (-4))\cdot (-8)) $
  4. $ -\left[(-6) \cdot ((-3)\cdot(-2-(-3)))\right]$
  1. $\frac{3}{4} \cdot \frac{2}{3}=\frac{1}{2}$
  2. $\frac{4}{8} \cdot \left(-\frac{3}{7}\right)=-\frac{3}{14}$
  3. $\frac{3}{9} \cdot \left(-6\right)=-2$
  4. $\left(-\frac{7}{11}\right) \cdot \left(-\frac{121}{49}\right)=\frac{11}{7}$
  1. $0,36 \cdot \frac{10}{6}=6$
  2. $\left(-0,8\right) \cdot \left(\frac{7}{4}\right)=-\frac{14}{10}=-1,4$
  3. $\left(-2,25\right) \cdot \left(-\frac{3}{15}\right)=\frac{45}{100}=0,45$
  4. $\left(-0,\bar{3}\right) \cdot 3=-1$
  1. $2,25 \cdot 4,1=9,225$
  2. $(-3,25) \cdot 6,3=-20,475$
  3. $(-0,36) \cdot (-2,2)=0,792$
  4. $6,75 \cdot (-1,24)=-8,37$
  1. $-\left((-3)-(-2) \right)=1$
  2. $-\left((-3)\cdot (-2) \right)=6$
  3. $-(2\cdot (-4))\cdot (-8))=-64 $
  4. $ -\left[ (-6) \cdot ((-3)\cdot 1)\right]=-18$


Aufgabe 9 Dividieren von Termen

Berechne die Terme. Denke daran: Man dividiert durch eine Zahl, indem man mit dem Kehrwert multipliziert.

  1. $\frac{8}{5} : \frac{3}{4}$
  2. $\frac{4}{8} : \left(-\frac{2}{6}\right)$
  3. $24 : \left(-6\right)$
  4. $6 : \left(-\frac{3}{2}\right)$
  1. $0,36 : \frac{6}{10}$
  2. $\left(-0,8\right) : \left(\frac{7}{4}\right)$
  3. $\left(-2,25\right) : \left(-\frac{5}{15}\right)$
  4. $\left(-0,\bar{3}\right) : 3$
  1. $2,25 : 4,1$
  2. $(-3,25) : 6,3$
  3. $(-0,36) : (-2,2)$
  4. $6,75 : (-1,24)$
  1. $\frac{8}{5} : \frac{3}{4} =\frac{32}{15} $
  2. $\frac{4}{8} : \left(-\frac{2}{6}\right)=-\frac{3}{2}$
  3. $24 : \left(-6\right)=-4$
  4. $6 : \left(-\frac{3}{2}\right)=-4$
  1. $0,36 : \frac{6}{10}=0,6$
  2. $\left(-0,8\right) : \left(\frac{7}{4}\right)=-\frac{14}{10}=-\frac{32}{70}$
  3. $\left(-2,25\right) : \left(-\frac{5}{15}\right)=6,75$
  4. $\left(-0,\bar{3}\right) : 3=-\frac{1}{9}$
  1. $2,25 : 4,1=\frac{225}{410}$
  2. $(-3,25) : 6,3=-\frac{325}{630}$
  3. $(-0,36) : (-2,2)=\frac{9}{55}$
  4. $6,75 : (-1,24)=-\frac{675}{124}$


Aufgabe 10 Eingebaute Fehler.

Tim und Tom rechnen. Na, hat sich da nicht der ein oder andere Fehler eingeschlichen?

  1. Rechne die Aufgabe zuerst selbständig.
  2. Finde die Fehler.
  3. Entscheide welche Lösung richtig ist.
  4. Finde deine Fehler.

Tim:

  1. $-2\left[6-3(4-2) \right]$$=-2\left[6-3\cdot 2 \right]$$=-2\cdot 0=0$
  2. $(-3)\cdot \left(\frac{1}{4} + \frac{1}{5} \cdot \frac{1}{3}\right)$$=(-3)\cdot \left(\frac{1}{4} + \frac{1}{15}\right)$$=(-3)\cdot \left(\frac{15}{60} + \frac{4}{60}\right)$$=(-3)\cdot \left(\frac{19}{60}\right)=-\frac{19}{60}$

Tom:

  1. $-2\left[6-3(4-2) \right]$$=-2\left[3\cdot 2 \right]$$=-12$
  2. $(-3)\cdot \left(\frac{1}{4} + \frac{1}{5} \cdot \frac{1}{3}\right)$$=(-3)\cdot \frac{1}{4} + \frac{1}{15}$$=-\frac{3}{4}+\frac{1}{15}$$=\frac{45}{60}+\frac{4}{60}=\frac{49}{60}$
  1. Tim hat richtig gerechnet.
  2. Tim hat richtig gerechnet.


Wortliste und Satzbausteine



der Term, -e mathematischer Ausdruck aus Zahlen und Rechenzeichen, wie $1+4$ oder $x+2$
die Variable, -n Ein Zeichen, welches für eine Zahl aus dem Zahlenbereich $\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$, oder $\mathbb{R}$ steht.
die natürlichen Zahlen $\mathbb{N}$ $0, 1, 2, 3 ...$
die ganzen Zahlen $\mathbb{Z}$ $\mathbb{N}$ und $-1, -2, -3,\:\dots$
die rationalen Zahlen $\mathbb{Q}$ $\mathbb{Z}$ und $\frac{1}{3}, 2.2, -1.45,\: ...$
die reellen Zahlen $\mathbb{R}$ $\mathbb{Q}$ und $\pi \: \dots$
die Zahlen­menge, -n Eine bestimmte Gruppe an Zahlen.
der Betrag einer Zahl, -"e einer Zahl Der Wert einer Zahl ohne Vorzeichen: $|-7|=7$ oder $|+7|=7$
die Änderung, -en Gibt die Distanz $\Delta$ (gr. Delta) zwischen zwei Punkten an.
Die Summe der natürlichen Zahlen von 1 bin n $\sum_{k=1}^{n}k=\frac{n}{2} \cdot (n+1)$ mit $k \in \mathbb{N}$
$k$ ist Element von $\mathbb{N}$ oder $k$ gehört zur Zahlenmenge $\mathbb{N}$ $k \in \mathbb{N}$
Gegenzahl, -enx Die Gegenzahl von +3 ist -3.
© mylime.info