Hypothesentest - Binomialverteilung
Aufgabe 1 Fehlerwahrscheinlichkeit
Ein neuer Laser soll statt 10 % Ausfälle nur noch 1 % Ausfälle haben. Um diese Hypothese zu bestätigen wird ein kritischer Wert von 5 Ausfällen bei einer Stichprobenmenge von 100 festgelegt. Das bedeutet, wenn weniger als 5 Laser ausfallen ist die Charge gut.
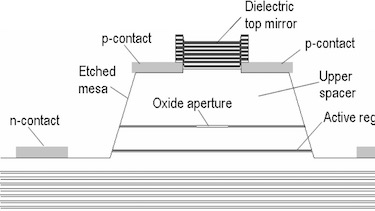
- Berechne den Erwartungswert für beide Ausfallswahrscheinlichkeiten.
- Berechne die Fehlerwahrscheinlichkeit 1. Art.
- Berechne die Fehlerwahrscheinlichkeit 2. Art.
- Berechne die Fehlerwahrscheinlichkeit 2. Art bei einem Stichprobenumfang von $n=200$. Passe den kritischen Wert entsprechend an.
- Beurteile: Wäre es sinnvoller den kritischen Wert auf 4 herabzusetzen?
- Wie hoch ist die Lebenserwartung eines Lasers in der Kommunikationstechnik und die zugehörige Ausfallwahrscheinlichkeit?
- Erwartungswerte:
$E(p=10\:\%)=10\:\%$
$E(p=1\:\%)=1\:\%$ - Fehler Nr. 1: Der Laser hat eine Ausfallwahrscheinlichkeit von 1 %. Es fallen aber 5 oder mehr Laser aus:
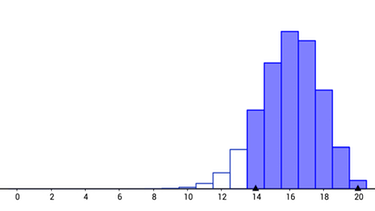
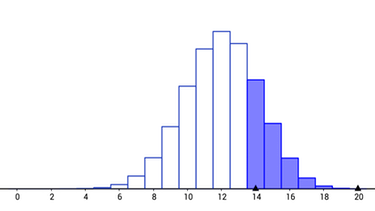
$P(X\geq 5)=0,34\: \%$ - Fehler Nr. 2: Der Laser hat eine Ausfallwahrscheinlichkeit von 10 %. Es fallen aber nur 4 oder weniger Laser aus:
$P(X\leq 4)=2,37\: \%$ - Fehler Nr. 2 bei $n=200$: Der Laser hat eine Ausfallwahrscheinlichkeit von 10 %. Es fallen aber nur 8 oder weniger Laser aus:
$P(X\leq 8)=0,14\: \%$ - Kritischer Wert = 4:
Fehler Nr. 1: $P(X\geq 4)=1,84\: \%$
Fehler Nr. 2: $P(X\leq 3)=0,78\: \%$
Der Fehler erster Art ist etwas erhöht, dafür aber der Fehler zweiter Art entsprechend geringer.
- Laser in der Kommunikationstechnik haben selbst bei Temperaturen von 85 °C eine Lebenserwartung von über 20 Jahren mit einer Ausfallwahrscheinlichkeit von 0,1 %.
Aufgabe 2 gezinkte Münze
Tina behauptet: "Diese Münze ist gezinkt. Zahl wird mit 60 % Wahrscheinlichkeit getroffen."
- Entwirf einen Testplan.
- Lege einen kritischen Wert fest.
- Berechne die Fehlerwahrscheinlichkeit 1. Art.
- Beschreibe welche Bedeutung die Fehlerwahrscheinlichkeiten haben und wie du sie reduzieren kannst.

Am besten du führst den Versuch mit einer Gruppe von Menschen durch. Wie wäre es mit deiner Klasse?
Tipp: Du kannst die Ranint(1,2)-Funktion am Taschenrechner nutzen, um das Experiment durchzuführen.
Aufgabe 3 Marketing
Der Bekanntheitsgrad eines Energydrinks ist umstritten. Während die Geschäftsführung von 70 % ausgeht, glaubt die Marketingabteilung nur an 40 %. Durch eine Stichprobe mit dem Umfang $n=50$ will man herausfinden, ob eine Werbekampange notwendig ist. Dabei darf der Fehler 1. Art höchstens $\alpha=10\:\%$ betragen.

- Berechne den Erwartungswert der Marketingabteilung und der Geschäftsführung.
- Berechne die Entscheidungsregel, die aus Sicht der Marketingabteilung getroffen werden muss.
- Berechne die Entscheidungsregel, die aus Sicht der Geschäftsführung getroffen werden muss.
- Bestimme die Wahrscheinlichkeit $\beta$ für die Marketingabteilung.
- Bestimme die Wahrscheinlichkeit $\beta$ für die Geschäftsführung.
- Beurteile: Welcher Test scheint sinnvoller?
- Marketingabteilung: $\mu = 50 \cdot 0,4 = 20$
Geschäftsführung: $\mu = 50 \cdot 0,7 = 35$ - Marketingabteilung:
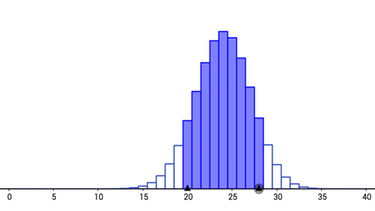
Angenommen der Bekanntheitsgrad liegt bei nur 40 %. Trotzdem kennen 25 oder mehr Personen den Energydrink: $\alpha=P(X\geq 25)=9,78\: \%$
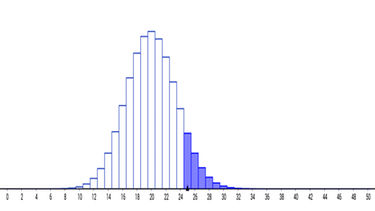
- Geschäftsführung:
Angenommen der Bekanntheitsgrad liegt bei 70 %. Trotzdem kennen nur 30 oder weniger Personen den Energydrink: $\alpha=P(X\leq 30)=8,48\: \%$

- Marketingabteilung:
Angenommen der Bekanntheitsgrad liegt bei 70 %. Trotzdem kennen nur 24 oder weniger Personen den Energydrink: $\beta=P(X\leq 24)=0,09\: \%$
- Geschäftsführung:
Angenommen der Bekanntheitsgrad liegt bei nur 40 %. Trotzdem kennen 31 oder mehr Personen den Energydrink: $\alpha=P(X\geq 31)=0,14\: \%$
Aufgabe 4 Haben Elefanten ein Gedächtnis?
Von Elephanten wird immer wieder berichtet, dass sie ein sehr gutes Gedächtnis haben. Um dies genauer zu untersuchen, lässt man ihnen an ihrem Gehege eine rechte und eine linke Öffnung und füttert ihnen jeweils Bananen. Nach einiger Zeit wiederholt man das Experiment und beobachtet, ob sie den rechten oder linken Ausgang verwenden. Der Versuch wird mit 100 Elefanten durchgeführt.
- Wie oft müssten die Ereignisse LL, RR, LR und RL auftreten, falls Elefanten kein Gedächtnis haben?
- Bestimme die Entscheidungsregel für die Hypothese Elefanten haben kein Gedächtnis bei einer Irrtumswahrscheinlichkeit von $\alpha \leq 10\:\%$.
- Wovon kann man ausgehen, falls Elefanten ein Gedächtnis haben?

- Die Ereignisse LL, RR müssten genauso oft auftreten wie LR und RL
- $P_{0,5}(41 \leq X \leq 59)=0,9431$
$P_{0,5}(42 \leq X \leq 58)=0,9114$
$P_{0,5}(43 \leq X \leq 57)=0,8668$
Die Elefanten haben kein Gedächtnis mit einer Irrtumswahrscheinlichkeit von $\alpha \leq 10\:\%$, falls zwischen 42 und 58 Elefanten LR oder RL als Ausgang wählen.
- Sollten Elefanten tatsächlich ein Gedächtnis haben können wir davon ausgehen, dass mindestens 59 Elefanten LL oder RR wählt.
Aufgabe 5 Standardabweichung
Bestimme die Standardabweichung.
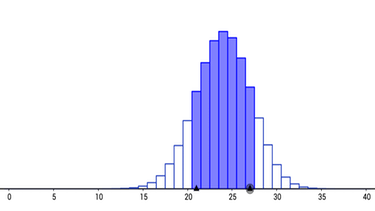
- Es wird $n=3$mal gewürfelt. Die 6 gilt als Treffer.
- Es wird $n=10$mal gewürfelt. Die 6 gilt als Treffer.
- Der Stichprobenumfang beträgt $n=40$ und die Trefferwahrscheinlichkeit $p=0,6$.
- Vervollständige die Tabelle für $n=100$:
$p$ 0,5 0,4 0,6 0,3 0,7 $\sigma$
- $\sigma = 0,6455$
- $\sigma = 1,1786$
- $\sigma = 3,0984$
- Tabelle für $n=100$:
$p$ 0,5 0,3 0,7 0,1 0,9 $\sigma$ 5 4,6 4,6 3 3
Aufgabe 6 Sigmaumgebung
Bei einem 400fachen Münzwurf gilt: $\mu = 200$ und $\sigma = 10$. Bestimme die Wahrscheinlichkeit bei der die Anzahl von "Zahl" in volgendem Intervall liegt:
- [160; 240]
- [175; 225]
- [180; 220]
- [$\mu - \sigma$; $\mu + \sigma$]
- [$\mu - 1,6\sigma$; $\mu + 1,6\sigma$]
- [$\mu - 3\sigma$; $\mu + 3\sigma$]

- $P(160 \leq X \leq 240)=1$
- $P(175 \leq X \leq 225)=0.9893$
- $P(180 \leq X \leq 220)=0.9745$
- $P(190 \leq X \leq 210)=0.833$
- $P(184 \leq X \leq 216)=0.9012$
- $P(170 \leq X \leq 230)=0.9978$
Wortliste und Satzbausteine
| der Erwartungswert, -e | der am häufigsten auftretende Wert bei einer Stichprobe: $\mu=n\cdot p$ |
| die Hypothese, -n | eine Vermutung |
| der Hypothesentest, -s | Versuch bei dem eine Vermutung (Hypothese), mit einer bestimmten Wahrscheinlichkeit bestätigt oder verworfen wird. |
| der kritische Wert, -e | Ergebnis, welches zum Testen einer Hypothese als Grenzwert festgelegt wird. |
| Fehler 1. Art $\alpha$, keine Mehrzahl | Obwohl die Hypothese wahr ist, verwirft das Testergebnis die Hypothese. |
| Fehler 2. Art $\alpha$, keine Mehrzahl | Obwohl die Hypothese falsch ist, bestätigt das Testergebnis die Hypothese. |
| die Irrtumswahrscheinlichkeit $\alpha$ und $\beta$, -n | die Wahrsscheinlichkeit für einen Fehler 1. und 2. Art |
| das LAPLACE-Experiment, -e | Ein Experiment wie der Münzwurf, bei dem es nur 2 Ereignisse gibt und beide Ereignisse mit einer Wahrscheinlichkeit von 50 % eintreten. |
| Der zweiseitige Binomialtest, -s | Ein Hypohesentest, bei welchem die Wahrscheinlichkeiten der Randbereiche der Binomialverteilung bestimmt werden. |
| Die Standardabweichung, -en | Ein Maß für die Streuung der Binomialverteilung um den Erwartungswert $\mu$: $\sigma = \sqrt{np(1-p)}$ |
| Die Sigmaumgebung, -en | Berechnung mit welcher Wahrscheinlichkeit das Ereignis im Bereich $\mu \pm \sigma$ liegt. |