mylime - Mathe

1 Anzahl an Stühlen - Flächen

Stelle alle Stühle im Klassenraum zu einer möglichst großen rechteckigen Fläche zusammen. Ermittle die Anzahl der Stühle indem du möglichst wenig Stühle zählst. Beantworte folgende Fragen:

Wie ändert sich die Fläche, wenn das Rechteck um eine Reihe erweitert wird?
Wie viele Reihen muss man dazu stellen damit sich die Fläche verdoppelt?
Worauf musst du beim Zählen der Reihen und Spalten achten?
Wie kann man den Umfang bestimmen

Notiere die Ergebnisse.

2 Flächeninhalte vergleichen

Das Quadrat, Rechteck und Parallelogramm sind gleich groß

Merke: Bestehen Figuren aus den gleichen Teilflächen, haben sie den identischen Flächeninhalt.

3 Maßzahl und Einheit

Ein Quadrat mit der Kantenlänge 1 cm hat den Flächeninhalt von 1 cm².

Merke: Zwischen Maßzahl und Einheit kommt ein Leerzeichen. Dieses darf nicht durch einen Zeilenumbruch getrennt werden.

Möchte man eine Fläche von 6 m² in cm² umrechnen geht man wie folgt vor:
Eine Fläche von 6 m² setzt sich bspw. zusammen aus einer Kantenlänge von 6 m und 1 m. Deshalb gilt:
$A=6\: \text{m} \cdot 1\: \text{m}= 600\: \text{cm} \cdot 100\: \text{cm} $ $=60.000\: \text{cm}^2$

Merke: Ein Quadrat mit einer Seitenlänge von 10 m hat eine Fläche von 1 a (Ar), mit 100 m eine Fläche von 1 ha (Hektar).

4 Mit Flächen rechnen

Man erhält den Flächeninhalt $A$ eines Rechtecks, wenn man die beiden Kantenlängen multipliziert:

$$A = a \cdot b$$

Den Umfang $u$ eines Rechtecks berechnet man mit:

$$u=a+b+a+b=2a+2b$$

5 Körper vergleichen

Die Skyline von Hongkong besteht aus vielen Wolkenkratzer. Es sind Körper mit unterschiedlichem Rauminhalt. Diesen Rauminhalt nennt man Volumen.

Ein Körper mit einer Länge von 70 cm, einer Breite von 40 cm und einer Höhe von 30 cm hat ein Volumgen von:

$$70\:cm \cdot 40\:cm \cdot 30\:cm=84.000\:cm^3$$

Verdoppelt man die Länge, verdoppelt sich das Volumen oder verdreifacht man die Höhe, verdreifacht sich auch das Volumen.

6 Messen und Umrechnen von Volumina

Ein Würfel mit der Kantenlänge 2 cm hat den Rauminhalt oder Volumen $V$ von $2\:cm \cdot 2\:cm \cdot 2\:cm =8\:cm^3$.

Dabei ist 8 die Maßzahl und cm³ die Maßeinheit. Die Einheit cm³ wird als Kubikcentimeter oder auch cbm bezeichnet.

Möchte man ein Volumen $V$ von 6 m³ in cm³ umrechnen geht man wie folgt vor:
$V=6\: \text{m} \cdot 1\: \text{m} \cdot 1\: \text{m}= 600\: \text{cm} \cdot 100\: \text{cm} \cdot 100\: \text{cm} $ $=6.000.000\: \text{cm}^3$

Beachte das 1 l ein Volumen von 1 dm³ hat, bzw. 1 m³ ein Volumen von 1000 l entsprechen.

7 Rechnen mit Volumina

Man erhält das Volumen $V$ eines Quaders, wenn man die Kantenlängen multipliziert:

$$V = a \cdot b \cdot c$$

Die Oberfläche $O$ eines Quaders berechnet man mit:

$$O=2ab+2ac+2bc$$

Ideen:
H. Griesel et al., "Elemente der Mathematik", Band 1, Schroedel Verlag, 2004

Aufgabe 1 Anzahl an Farbdosen und Karokästchen

Eine Farbpalette hat in einer Reihe 12 und in einer Spalte 7 Dosen. Berechne die Anzahl der Dosen.

Berechne die Anzahl von Karokästchen auf einem DIN A4 Blatt.

Berechne die Fläche eines Schultisches.
Wie groß ist die Fläche aller Schultische in einem Klassenzimmer?

Berechne die Fläche eines Kästchens wenn der Zauberwürfel eine Kantenlänge von 4 cm hat.

Die Farbpalette hat $12\cdot 7 = 84$ Dosen.

Ein DIN A4 Blatt hat 2748 Kästchen, wenn man die halben Kästchen am Rand addiert.

Ein Schultisch hat beispielweise eine Fläche von: $A=50\cdot 130=6.500\:\text{cm}^2$. Bei 12 Tischen im Raum macht dies eine Gesamtfläche von $A=12\cdot 6.500=78.000\:\text{cm}^2$

Der Zauberwürfel:
Eine Seite hat $3\cdot 3 = 9$ Kästchen.
Insgesamt hat der Würfel $6 \cdot 9=54$ Kästchen.
Die Seitenfläche eines Würfels beträgt: $4\cdot 4=16$ cm² und ein Kästchen hat eine Fläche von $16:9=16/9$ cm².
Die Gesamtfläche des Würfels beträgt $16/9\cdot 54=96$ cm².

Aufgabe 2 Rasenflächen

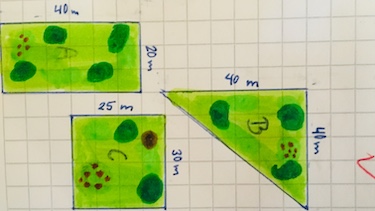
Die drei Rasenflächen sollen neu eingesäht werden. Vergleiche die Rasenflächen und gib an bei welcher die geringste Grassamenmenge benötigt wird.

A: $a=40\:$m, $b=20\:$m
B: $a=40\:$m, $b=40\:$m
C: $a=25\:$m, $b=30\:$m

$A_A=40 \cdot 20 = 800\:$m²
$A_B=40 \cdot 40 :2 = 800\:$m²
$A_C=25 \cdot 30 = 750\:$m²

Bei der Rasenfläche C wird die geringste Menge an Grassamen benötigt.

Aufgabe 3 Maßzahl und Maßeinheit

Korrigiere den Text: Der Boden hat eine Fläche von 4
cm². Die Kantenlänge ist 2cm. Die gleiche Fläche hat ein Rechteck mit einer Kantenlänge von 1 cm und 4 cm.
Berechne 4 km² in m².
Berechne 12 m² in cm².
Berechne 5 km² in m².
Berechne 4 km² in cm².
Berechne 13 m² in cm².
Berechne 14 m² in dm².
Berechne 125 m² in cm².

Der Boden hat eine Fläche von 4 cm². Die Kantenlänge ist 2 cm. Die gleiche Fläche hat ein Rechteck mit einer Kantenlänge von 1 cm und 4 cm.
$A=4\: km \cdot 1\:km$ $= 4000\: m \cdot 1000\: m$ $=4.000.000\: m^2$
$A=12\: m \cdot 1\:m$ $= 1200\: cm \cdot 100\: cm$ $=120.000\:cm^2$
$A=5\: km \cdot 1\:km$ $= 5000\: m \cdot 1000\: m$ $=5.000.000\:m^2$
$A=4\: km \cdot 1\:km$ $= 4.000\: m \cdot 1.000\: m$ $= 400.000\: cm \cdot 100.000\: cm$ $=40.000.000.000\:cm^2$
$A=13\: m \cdot 1\:m$ $= 1300\: cm \cdot 100\: cm$ $=130.000\:cm^2$
$A=14\: m \cdot 1\:m$ $= 140\: dm \cdot 10\: dm$ $=1.400\:cm^2$
$A=125\: m \cdot 1\:m$ $= 12500\: cm \cdot 100\: cm$ $=1.250.000\:cm^2$

Aufgabe 4 Ar und Hektar

Ein Einfamilienhaus (EFH) benötigt eine Grundstücksfläche von 500 m². Berechne die Anzahl an EFH auf einer Fläche von

1 ha,
1 a,
1 km².

Gib die Seitenlängen der folgenden Quadrate an:

36 ha, 64 a, 49 km².
Ein Gärtner will einen 18 a großen Acker einsäen. Für je 1 m² Fläche benötigt er 25 g Grassamen. Berechne die notwendige Menge an Grassamen.
Ein Landwirt baut auf auf einer Fläche von 6 ha Weizen an. Pro 100 m² Fläche benötigt man 1,2 kg Saatgut. Berechne die Saatgutmenge

1 ha: $10.000/500=20$ Häuser,
1 a: $100/500\: \Rightarrow$ passt nicht drauf,
1 km²: $1.000.000/500=2000$ Häuser.
600 m, 80 m, 7 km
$A=18\:a=18\cdot 10\: m \cdot 10\:m$ $= 1800\: m^2$
Menge an Grassamen $= 25\: g \cdot 1800 = 45.000\:g$
$A=6\:ha=6\cdot 100\: m \cdot 100\:m$ $= 60.000\: m^2$
Menge an Weizen $= 1,2\: kg \cdot 60.000 :100 = 720\:kg$

Aufgabe 5 Umrechnen der Maßeinheiten

Berechne in cm³.

4 m³
2.000 mm³
1 l

Berechne in mm³.

14 m³
20 cm³
4 l

4 m³ = 4.000.000 cm³
2.000 mm³ = 2 cm³
1 l = 1.000 cm³
14 m³ = 14.000.000.000 mm³
20 cm³ = 20.000 mm³
4 l = 4.000.000 mm³

Aufgabe 6 Fehlende Größen

Berechne die fehlende Größen des Quaders

Länge a	Breite b	Höhe c	Volumen V	Oberfläche O
4	2	1
12	8	2
4	2		16
3	2			62

Länge a	Breite b	Höhe c	Volumen V	Oberfläche O
4	2	1	8	28
12	8	2	192	272
4	2	2	16	40
3	2	5	30	62

Wortliste und Satzbausteine

der Flächeninhalt, -e	Maß für die Größe einer Fläche
das Rechteck, -e	eine geometrische Figur mit vier rechten Winkeln (90 °)
das Quadrat, -e	ein Rechteck mit vier gleich langen Seiten
der Flächeninhalt eines Rechtecks	Der Flächeninhalt $A$ eines Rechtecks berechnet sich aus den Kantenlängen $a$ und $b$ zu: $A_{\square}=a\cdot b$
der Umfang eines Rechtecks	Der Umfang $u$ eines Rechtecks berechnet sich zu: $u=2a+2b$
die Maßeinheit des Flächeinhalts, -en	Der Flächeninhalt wird in m² gemessen. Es gilt: 1 m² = 10.0000 cm².

das Volumen, Volumina	Das Volumen ist die Größe des ausgefüllten Raumes. Es wird in Kubikmeter (m³) oder Liter (l) gemessen.
die Oberfläche, -n	Die Oberfläche eines Körpers ist der Flächeninhalt aller Teilflächen.
die Palette, -n	eine rechteckige Konstruktion, die den Transport einer Vielzahl an Waren ermöglicht
die Reihe, -n	die waagerechte Anordnung von Gegenständen oder Werten
die Spalte, -n	die senkrechte Anordnung von Gegenständen oder Werten.
der Landwirt, -e	ein Bauer oder eine Bäuerin
der Grassamen, ~	Fortpflanzungsorgan von Gras
das Saatgut, -"er	der Samen

Flächen- und Rauminhalte