Zwei sich schneidende Geraden

Schnittpunkte von Geraden

17.05.2015

Wer Schnittpunkte von Geraden berechnen kann ist bspw. in der Lage Netztarife mit Grundgebühr zu vergleichen.

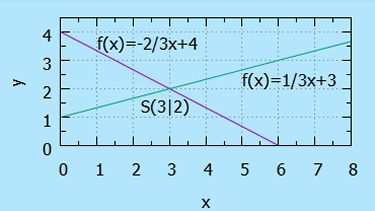
Funktionsschaubild zweier Geraden

Die Schnittpunkte einer Geraden mit den Achsen nennt man die Nullstellen Nx und Ny:

Bedingung für Nx: $$f(x)=0 $$
Bedingung für Ny: $$x=0$$

Der Schnittpunkt zweier Geraden erhält man durch Gleichsetzen der beiden Funktionsgleichungen und entprechendes Einsetzen.

xS-Wert bestimmen (Gleichsetzen): $$f_1(x)=f_2(x)$$
yS-Wert bestimmen (Einsetzen): $$f_1(x_S) \lor f_2(x_S)$$

Aufgabe 1

  1. Bestimme den Schnittpunkt der beiden Funktionen $f(x)=-2x+9$ und $g(x)=1/3x+2$.

  2. Zeichne die beiden Funktionen.

  1. Gleichsetzen:
    $f(x)=g(x)$
    $-2x+9=1/3x+2$
    $-6x+27=x+6$
    $21=7x$
    $x=3$

    Einsetzen:
    $y=f(3)=-2\cdot 3 +9=3$

    Lösungsmenge: $L=\{ 3;3 \} $

  2. Schaubild der Funktionen:


Aufgabe 2

Gegeben sind die Funktionen $f(x)=1/4x+2$ und $g(x)=-1/2x+1$.

  1. Bestimme den exakten Schnittpunkt der beiden Funktionen.

  2. Lena rechnet:
    $\frac{1}{4}x+2=-\frac{1}{2}x+1~~~|+\frac{1}{2}x-2$
    $\frac{2}{6}x=-1~~~|\cdot3$
    $x=-3$
    Welchen Fehler hat Lena gemacht?

  1. Gleichsetzen:
    $f(x)=g(x)$
    $1/4x+2=-1/2x+1~|\cdot 4$
    $x+8=-2x+4~|+2x-8$
    $3x=-4~|:3$
    $x=-4/3$

    Einsetzen:
    $f(-4/3)=1/4\cdot (-4/3)+2=-4/12+2=20/12=10/6=5/3$

    Lösung:
    $S(-\frac{4}{3};\frac{5}{3})$

  2. Man darf Brüche nur mit dem gleichen Nenner addieren.


Aufgabe 3

Gegeben ist $h(x)=2x+2$ und $i(x)=-x+4$.

  1. Bestimme den Schnittpunkt zeichnerisch.

  2. Bestimme den exakten Schnittpunkt rechnerisch.

  1. Zeichnerische Lösung: S(0,7|3,3)

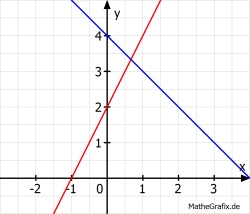
  2. Gleichsetzen:
    $h(x)=i(x)$
    $2x+2=-x+4~|+x-2$
    $3x=2~|:3$
    $x=2/3$

    Einsetzen:
    $h(2/3)=2\cdot (2/3)+2=4/3+2=10/3$
    $i(2/3)=-2/3+4=-2/3+12/3=10/3$

    Schnittpunkt:
    $S=\{ 2/3;10/3 \}=\{ 0,67;3,33 \} $
    Vergleicht man die beiden Lösungen, sieht man, dass man auch zeichnerisch schon relativ nah am exakten Wert liegt.


Aufgabe 4 - Achsenschnittpunkte

Gegeben ist $f(x)=-\frac{3}{4}x+6$.

  1. Berechne den Schnittpunkt mit der x-Achse.

  2. Berechne den Schnittpunkt mit der y-Achse.

  1. Nx:
    $\begin{align} f(x)&=0\\ \Leftrightarrow -\frac{3}{4}x+6&=0~~|-6\\ \Leftrightarrow -\frac{3}{4}x&=-6~~|\cdot (-4/3)\\ \Leftrightarrow x&=8\\ &\Rightarrow N_x(8|0)\\ \end{align}$

  2. Ny:
    $\begin{align} x&=0\\ \Leftrightarrow f(0)&=-\frac{3}{4}\cdot 0+6\\ \Leftrightarrow f(0)&=6\\ &\Rightarrow N_y(0|6)\\ \end{align}$


Aufgabe 5 - Anwendungsaufgabe

Für den Autoführerschein liegen Manuel zwei Angebote vor.

Angebot 1:
Grundgebühr: 150,-€
Preis pro Fahrstunde: 25,-€
Angebot 2:
Grundgebühr: 0,-€
Preis pro Fahrstunde: 35,-€

  1. Stelle für jedes Angebot eine Funktionsgleichung auf.

  2. Ermittle die jeweiligen Fahrtkosten bei 6 Fahrstunden.

  3. Bei wie vielen Fahrstunden sind die Kosten identisch?

  1. Funktionsgleichungen (x: Fahrstungen, y: Kosten)

    Angebot 1:
    $f_1(x)=25x+150$
    Angebot 2:
    $f_2(x)=35x$

  2. Kosten nach 6 Fahrstunden

    Angebot 1:
    $f_1(6)=300$
    Angebot 2:
    $f_2(6)=210$

  3. Schnittpunkt der Kosten:
    Durch Gleichsetzen der beiden Funktionen erhält man den Kostenschnittpunkt:
    $\begin{align} f_1(x)&=f_2(x)\\ \Leftrightarrow 25x+150&=35x~~|--25x\\ \Leftrightarrow 150&=10x~~|:10\\ \Leftrightarrow x&=15\\ \end{align}$

    Antwort: Bei 15 Fahrstunden sind die Kosten genau gleich.



Aufgabe 6 - Aufstellen von Geradengleichungen

Bestimme die Funktionsvorschrift, sowie die Nullstellen

  1. Der Punkt A(2|4) liegt auf dem Graphen der linearen Funktion $f(x)=-2x+b$.

  2. Die Punkte A(0,4|1) und B(1|0,4) liegen auf dem Graphen der linearen Funktion $f$.

  3. Der Graph einer linearen Funktion geht durch den Punkt A(3|1) und hat die Nullstelle 1.

  4. Der Graph einer linearen Funktion hat die Nullstelle 2 und die Steigung 4.

  1. $f(x)=-2x+8$
    $N_x(4|0)$, $N_y(0|8)$

  2. $f(x)=-x+1,4$
    $N_x(1,4|0)$, $N_y(0|1,4)$

  3. $f(x)=0,5x+-0,5$
    $N_x(1|0)$, $N_y(0|-0,5)$

  4. $f(x)=4x-8$
    $N_x(2|0)$, $N_y(0|-8)$


Wortliste und Satzbausteine



die lineare Funktion, -en eine Funktion mit der Form: $f(x) = mx + b$, mit $a$ ungleich Null
der Funktionswert $f(x)$, -e der zugehörige Wert zu der Funktionsstelle $x$.
die Gerade, -n das Schaubild/der Graf der linearen Funktion, man erhält diesen indem man die einzelnen Wertepaare aus Funktionstelle und Funktionswert in einem Koordinatensystem aufträgt.
die Nullstelle, -n der Schnittpunkt mit der x-Achse
der y-Achsen­abschnitt $b$, -e der Schnittpunkt der Geraden mit der y-Achse. Man erhält ihn indem man $f(0)$ berechnet
die Steigung $m$, -en ein Maß für die Steilheit/Anstieg einer Geraden: $m=\frac{\Delta y}{\Delta x}$
die Distanz $\Delta$, -en $\Delta y$ - Distanz in y-Richtung, $\Delta x$ - Distanz in x-Richtung
der Schnittpunkt zweier Geraden Gemeinsamer Punkt von Gerade 1 und Gerade 2
© mylime.info