Ebenen eines Hauses

Analytische Geometrie - Ebenen

Die Darstellung einer Ebene in Parameter- und Koordinatenform sowie die Lagebeziehung zwischen Ebenen und Geraden wird erklärt.

1 Ebenen
Ebenen eines Hauses

Häuser haben verschiedene Ebenen. Zeichne eine 3D Ansicht eines Hauses mit Pultdach und gib die Koordinaten von drei Punkten an, die auf der Dachfläche liegen.

Markiere parallele Geraden oder Flächen auf einem Bild. Beschreibe die Ebenen.

enaktiv

2 Parameterdarstellung einer Ebene

Definition: Man nennt E: $\vec{x} = \vec{OA} + s\cdot\vec{u} + t\cdot\vec{v}$ mit $s, t \in \mathbb{R}$ und $\vec{u} \nparallel \vec{v}$ eine Para­me­ter­dar­stellung der Ebene mit den Parametern $s$ und $t$, dem Ortsvektor $\vec{OA}$ sowie den Richtungsvektoren $\vec{u}$ und $\vec{v}$.

Die drei Punkte $A(1|2|0)$, $B(4|2|3)$, $C(7|3|3)$ mit den Richtungsvektoren $\vec{AB}=(3|0|3)$ und $\vec{AC}=(6|1|3)$ liegen auf der Ebene E:

$$\vec{x}=\left(\begin{array}{c} 1 \\ 2 \\ 0 \end{array}\right) + s\cdot \left(\begin{array}{c} 3 \\ 0 \\ 3 \end{array}\right) + t\cdot \left(\begin{array}{c} 6 \\ 1 \\ 3 \end{array}\right)$$
3 Punktprobe in der Ebene

Für die Ebene E in Paremeterform: $\vec{x}=\left(\begin{array}{c} 1 \\ 1 \\ 2 \end{array}\right) + s\cdot \left(\begin{array}{c} 2 \\ 0 \\ 1 \end{array}\right) + t\cdot \left(\begin{array}{c} 0 \\ 1 \\ 3 \end{array}\right)$ soll geprüft werden, ob der Punkt $P(2|4|8)$ in der Ebene liegt.

Lösungshinweis: Ebene mit Punkt gleichsetzten, LGS aufstellen, Parameter aus 2 Gleichungen bestimmen und dann in die dritte Gleichung einsetzen. Falls es eine wahre Aussage gibt, liegt der Punkt auf der Ebene.

4 Koordinatenform der Ebene

Die Ebene E in Paremeterform $\vec{x}=\left(\hspace{-0.5mm}\begin{array}{c} 2 \\ 1 \\ 1 \end{array}\hspace{-0.5mm}\right) + s\cdot \left(\hspace{-1.1mm}\begin{array}{c} 1 \\ 1 \\ -1 \end{array}\hspace{-1.1mm}\right) + t\cdot \left(\hspace{-1.2mm}\begin{array}{c} 1 \\ -1 \\ 3 \end{array}\hspace{-1.2mm}\right)$ soll auf die Koordinatenform gebracht werden.

Lösungshinweis: Wir erstellen aus der Ebene ein LGS, eleminieren mit dem Additionsverfahren die beiden Parameter und erhalten eine Gleichung mit $x_1$, $x_2$, $x_3$. Dies ist die Koordinatenform der Ebene E:

$$-2x_1 + 5x_2 + 3x_3 = 4$$
5 Lagebeziehung zwischen Ebene und Gerade

Hier wird erklärt wie man die Lage zwischen Ebene und Gerade in Parameterform ermittelt.

Grundsätzlich gibt es drei Möglichkeiten: g schneidet E in einem Schnittpunkt, g liegt in E (g $\in$ E) und g ist parallel zu E (g $\parallel$ E).

Lösungststrategie:

  1. Gleichsetzen und LGS lösen.
  2. Die Parameter in die Geraden- oder Ebenengleichung einsetzen.
6 Lagebeziehung zwischen zwei Ebenen 1

Schneiden sich zwei Ebenen bilden sie immer eine gemeinsamme Schnittgerade. Sind sie parallel zu einander, berühren sie sich in keinem Punkt und liegen sie direkt aufeinander, berühren sich sich in allen Punkten.

Lösungsstrategie, falls Ebene E1 in Parameterform und E2 in Koordinatenform gegeben ist:

  1. E1 als LGS schreiben.
  2. x1, x2, x3 aus LGS in E2 einsetzen.
  3. Nach einem der Parameter umstellen und in E1 einsetzen.
7 Lagebeziehung zwischen zwei Ebenen 2

E1: $\vec{x}=\left(\hspace{-0.5mm}\begin{array}{c} 2 \\ 0 \\ 4 \end{array}\hspace{-0.5mm}\right) + s\cdot \left(\hspace{-1.1mm}\begin{array}{c} 3 \\ 1 \\ 0 \end{array}\hspace{-1.1mm}\right) + t\cdot \left(\hspace{-1.2mm}\begin{array}{c} -1 \\ 0 \\ 1 \end{array}\hspace{-1.2mm}\right)$ und E2: $2x_1+x_2-x_3=1$

Mit $s=1/7+3/7t$ berechnet sich die Schnittgerade g der beiden Ebenen E1, E2 zu:
g: $\vec{x}=\left(\hspace{-0.5mm}\begin{array}{c} 17/7 \\ 1/7 \\ 4 \end{array}\hspace{-0.5mm}\right) + t\cdot \left(\hspace{-1.1mm}\begin{array}{c} 2/7 \\ 3/7 \\ 1 \end{array}\hspace{-1.1mm}\right)$

Ideen:
D. Jung, danieljung.education
H. Griesel et al, "Elemente der Mathematik", Bildungshaus Schulbuchverlage, 2010



Aufgabe 1 Parameterdarstellung der Ebene

Bestimme die Parameterform der Ebene, in welcher die Punkte A(3|2|1), B(6|4|3) und C(-2|4|-7) liegen.

Welchen Fehler haben Jan und Peter bei der Angabe der Parameterform gemacht?

Jan: $\quad\vec{x}=\left(\begin{array}{c} 3 \\ 2 \\ 1 \end{array}\right) + s\cdot \left(\begin{array}{c} 6 \\ 4 \\ 3 \end{array}\right) + t\cdot \left(\begin{array}{c} -2 \\ 4 \\ -7 \end{array}\right)$

Peter: $\quad\vec{x}=\left(\begin{array}{c} 3 \\ 2 \\ 1 \end{array}\right) + s\cdot \left(\begin{array}{c} -3 \\ -2 \\ -2 \end{array}\right) + t\cdot \left(\begin{array}{c} 5 \\ -2 \\ 8 \end{array}\right)$


$\vec{x}=\left(\begin{array}{c} 3 \\ 2 \\ 1 \end{array}\right) + s\cdot \left(\begin{array}{c} 3 \\ 2 \\ 2 \end{array}\right) + t\cdot \left(\begin{array}{c} -5 \\ 2 \\ -8 \end{array}\right)$ mit $s,t \in \mathbb{R}$

Jan hat nur die Punkte eingesetzt und nicht die Richtungsvektoren ausgrechnet, Peter hat die Richtungsvektoren $\vec{BA}$ und $\vec{CA}$ berechnet. Hinweis: Die Ebene von Peter ist identisch, da $s,t \in \mathbb{R}$.


Aufgabe 2 Punktprobe in der Ebene

Prüfe welche der folgenden Punkte in der Ebene $\vec{x}=\left(\begin{array}{c} 1 \\ 2 \\ 3 \end{array}\right) + s\cdot \left(\begin{array}{c} 3 \\ -4 \\ 0 \end{array}\right) + t\cdot \left(\begin{array}{c} 6 \\ 4 \\ 3 \end{array}\right)$ mit $s,t \in \mathbb{R}$ liegen.

  1. A(4|-2|3),
  2. B(7|-1|4),
  3. C(7|6|6).

Die Punkte A und C liegen in der Ebene.


Aufgabe 3 Parameterdarstellung bestimmen

Bestimme die Parameterdarstellung der Ebenen.


  1. Ebene mit Spurpunkten


  1. Ebene mit Spurpunkten


  1. $\vec{x}=\left(\hspace{-1.5mm}\begin{array}{c} -1 \\ 2 \\ 0 \end{array}\hspace{-1.5mm}\right)\hspace{-1mm}+ \hspace{-1mm}s\hspace{-1mm}\cdot\hspace{-1mm} \left(\hspace{-1.5mm}\begin{array}{c} 3 \\ -4 \\ 2 \end{array}\hspace{-1.5mm}\right)\hspace{-1mm} + \hspace{-1mm}t\hspace{-1mm}\cdot\hspace{-1mm} \left(\hspace{-1.5mm}\begin{array}{c} -2 \\ 0 \\ 4 \end{array}\hspace{-1.5mm}\right)$ mit $s,t \in \mathbb{R}$

  2. $\vec{x}=\left(\hspace{-1.5mm}\begin{array}{c} -2 \\ 3 \\ 4 \end{array}\hspace{-1.5mm}\right)\hspace{-1mm} + \hspace{-1mm}s\hspace{-1mm}\cdot\hspace{-1mm} \left(\hspace{-1.5mm}\begin{array}{c} -4 \\ 3 \\ 4 \end{array}\hspace{-1.5mm}\right)\hspace{-1mm} +\hspace{-1mm} t\hspace{-1mm}\cdot\hspace{-1mm} \left(\hspace{-1.5mm}\begin{array}{c} -2 \\ 0 \\ 4 \end{array}\hspace{-1.5mm}\right)$ mit $s,t \in \mathbb{R}$


Entspann dich erstmal ...

Schrägbild einer Ebene

Bestimmung der Spurpunkte aus der Koordinatenform

Die Spurpunkte sind die Schnittpunkte der Ebene mit den Achsen $x_1$, $x_2$, $x_3$.

Gegegeben ist die Ebene in Koordinatenform $6x_1+4x_2+3x_3=12$. Beim Schnittpunkt mit der $x_1$-Achse gilt: $x_2=x_3=0$

Somit gilt für den ersten Spurpunkt, den Schnittpunkt mit der $x_1$-Achse: $x_1=2$. Entsprechend lassen sich die beiden anderen Spurpunkte bestimmen:
$S_1(2|0|0)$, $S_2(0|3|0)$, $S_3(0|0|4)$

Aufgabe 4 Koordinatendarstellung und Schrägbild

Berechne die Koordinatendarstellung, bestimme die Spurpunkte und zeichne das Schrägbild.


  1. $\vec{x}=\left(\hspace{-1.5mm}\hspace{-1mm}\begin{array}{c} -1 \\ 2 \\ 0 \end{array}\hspace{-1.5mm}\right) + s\cdot \left(\hspace{-1.5mm}\begin{array}{c} 3 \\ -4 \\ 2 \end{array}\hspace{-1.5mm}\right) + t\cdot \left(\hspace{-1.5mm}\begin{array}{c} -2 \\ 0 \\ 4 \end{array}\hspace{-1.5mm}\right)$ mit $s,t \in \mathbb{R}$

  2. $\vec{x}=\left(\hspace{-1.5mm}\begin{array}{c} -2 \\ 3 \\ 4 \end{array}\hspace{-1.5mm}\right) + s\cdot \left(\hspace{-1.5mm}\begin{array}{c} -4 \\ 3 \\ 4 \end{array}\hspace{-1.5mm}\right) + t\cdot \left(\hspace{-1.5mm}\begin{array}{c} -2 \\ 0 \\ 4 \end{array}\hspace{-1.5mm}\right)$ mit $s,t \in \mathbb{R}$


$$2x_1 +3x_2 - x_3=0 \quad\quad S_2(0|-3|0)$$ $$\quad\quad -7x_1+x_2+3x_3=1 \quad$$ $$S_1(1|0|0) \quad\quad\quad -2x_1+x_2-x_3=12$$

  1. $x_1+x_2+\frac{1}{2}x_3=1$
    $S_1(1|0|0)$, $S_2(0|1|0)$, $S_3(0|0|2)$

    Ebene mit Spurpunkten

  1. $-\frac{1}{2}x_1+\frac{1}{3}x_2+\frac{1}{4}x_3=1$
    $S_1(2|0|0)$, $S_2(0|3|0)$, $S_3(0|0|4)$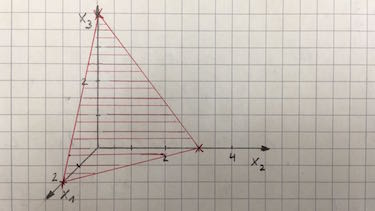

    Ebene mit Spurpunkten


Aufgabe 5 Lagebeziehung zwischen Ebene und Gerade

Untersuche die Lage von g und E und bestimme gegebenfalls den Schnittpunkt. Es gilt, mit $r,s,t \in \mathbb{R}$.


  1. g: $\vec{x}=\left(\hspace{-1.5mm}\hspace{-1mm}\begin{array}{c} -1 \\ 2 \\ 0 \end{array}\hspace{-1.5mm}\right) + r\cdot \left(\hspace{-1.5mm}\begin{array}{c} 3 \\ -4 \\ 2 \end{array}\hspace{-1.5mm}\right)$
    E: $\vec{x}=\left(\hspace{-1.5mm}\hspace{-1mm}\begin{array}{c} -1 \\ 2 \\ 0 \end{array}\hspace{-1.5mm}\right) + s\cdot \left(\hspace{-1.5mm}\begin{array}{c} 3 \\ -4 \\ 2 \end{array}\hspace{-1.5mm}\right) + t\cdot \left(\hspace{-1.5mm}\begin{array}{c} -2 \\ 0 \\ 4 \end{array}\hspace{-1.5mm}\right)$

  2. g: $\vec{x}=\left(\hspace{-1mm}\begin{array}{c} 3 \\ 2 \\ 1 \end{array}\hspace{-1mm}\right) + r\cdot \left(\hspace{-1.5mm}\begin{array}{c} 1 \\ -1 \\ 0 \end{array}\hspace{-1.5mm}\right)$
    E: $\vec{x}=\left(\hspace{-1.5mm}\begin{array}{c} 2 \\ 0 \\ -1 \end{array}\hspace{-1.5mm}\right) + s\cdot \left(\hspace{-1mm}\begin{array}{c} 2 \\ 1 \\ 1 \end{array}\hspace{-1mm}\right) + t\cdot \left(\hspace{-1.5mm}\begin{array}{c} -1 \\ 3 \\ 1 \end{array}\hspace{-1.5mm}\right)$

  1. g: $\vec{x}=\left(\hspace{-1mm}\begin{array}{c} -1 \\ -2 \\ -4 \end{array}\hspace{-1mm}\right) + r\cdot \left(\hspace{-1mm}\begin{array}{c} 1 \\ 0 \\ 1 \end{array}\hspace{-1mm}\right)$
    E: $\vec{x}=\left(\hspace{-1.5mm}\begin{array}{c} 4 \\ -1 \\ 3 \end{array}\hspace{-1.5mm}\right) + s\cdot \left(\hspace{-1mm}\begin{array}{c} 2 \\ 1 \\ -1 \end{array}\hspace{-1mm}\right) + t\cdot \left(\hspace{-1mm}\begin{array}{c} 3 \\ 1 \\ 0 \end{array}\hspace{-1mm}\right)$

  1. Das LGS ergibt die Lösung $0=0$. Aus diesem Grund liegt die Gerade g in der Ebene E.

  2. Das LGS ergibt die Lösung $r=-6$, $s=-1$, $t=3$. Das bedeutet die Gerade und die Ebene schneiden sich. Durch einsetzen erhält man den gemeinsammen Schnittpunkt: $S(-3|8|1)$

  1. Das LGS ergibt die Lösung $0=13$. Das bedeutet, es gibt keinen Schnittpunkt zwischen Gerade und Ebene. Somit sind Gerade und Ebene parallel zueinander: g $\parallel$ E.


Aufgabe 6 Lagebeziehung zwischen zwei Ebenen

Untersuche die Lage von E1 und E2 und bestimme gegebenfalls die Schnittgerade. Es gilt, mit $s,t,u,v \in \mathbb{R}$.


  1. E1: $\vec{x}=\left(\hspace{-1.5mm}\begin{array}{c} 1 \\ 1 \\ 1 \end{array}\hspace{-1.5mm}\right) + s\cdot \left(\hspace{-1.5mm}\begin{array}{c} 4 \\ 0 \\ 0 \end{array}\hspace{-1.5mm}\right) + t\cdot \left(\hspace{-1.5mm}\begin{array}{c} 2 \\ 2 \\ -2 \end{array}\hspace{-1.5mm}\right)$
    E2: $\vec{x}=\left(\hspace{-1mm}\begin{array}{c} 3 \\ 6 \\ 7 \end{array}\hspace{-1mm}\right) + u\cdot \left(\hspace{-1.5mm}\begin{array}{c} 2 \\ -2 \\ -2 \end{array}\hspace{-1.5mm}\right) + v\cdot \left(\hspace{-1.5mm}\begin{array}{c} 3 \\ 3 \\ -3 \end{array}\hspace{-1.5mm}\right)$

  2. E1: $\vec{x}=\left(\hspace{-1.5mm}\begin{array}{c} 2 \\ 0 \\ 4 \end{array}\hspace{-1.5mm}\right) + s\cdot \left(\hspace{-1.5mm}\begin{array}{c} 3 \\ 1 \\ 0 \end{array}\hspace{-1.5mm}\right) + t\cdot \left(\hspace{-1.5mm}\begin{array}{c} -1 \\ 0 \\ 1 \end{array}\hspace{-1.5mm}\right)$
    E2: $2x_1+x_2-x_3=1$

  3. E1: $3x_1-2x_2+x_3=10$
    E2: $2x_1+2x_2-2x_3=-2$

  1. E1: $\vec{x}=\left(\hspace{-1.5mm}\begin{array}{c} -1 \\ -2 \\ -1 \end{array}\hspace{-1.5mm}\right) + r\cdot \left(\hspace{-1.5mm}\begin{array}{c} 2 \\ 0 \\ 0 \end{array}\hspace{-1.5mm}\right) + s\cdot \left(\hspace{-1.5mm}\begin{array}{c} 1 \\ 1 \\ -1 \end{array}\hspace{-1.5mm}\right)$
    E2: $\vec{x}=\left(\hspace{-1mm}\begin{array}{c} 1 \\ 2 \\ 1 \end{array}\hspace{-1mm}\right) + t\cdot \left(\hspace{-1.5mm}\begin{array}{c} 1 \\ -2 \\ -4 \end{array}\hspace{-1.5mm}\right) + u\cdot \left(\hspace{-1.5mm}\begin{array}{c} -1 \\ 1 \\ -3 \end{array}\hspace{-1.5mm}\right)$

  1. 1. Aufstellen des LGS:
    \begin{array}{cccc} 4s &+2t &+2u &+3v &=2 \\ &+2t &-2u &+3v &=5 \\ &-2t &-2u &-3v &=6 \end{array}
    Das LGS ergibt die Lösung: $0=8$.

    Da die Aussage falsch ist, schneiden sich die Ebenen nicht und sind somit parallel.

  2. Mit $s=1/7+3/7t$ berechnet sich die Schnittgerade g der beiden Ebenen E1, E2 zu:
    g: $\vec{x}=\left(\hspace{-0.5mm}\begin{array}{c} 17/7 \\ 1/7 \\ 4 \end{array}\hspace{-0.5mm}\right) + t\cdot \left(\hspace{-1.1mm}\begin{array}{c} 2/7 \\ 3/7 \\ 1 \end{array}\hspace{-1.1mm}\right)$

  3. 1. Addition beider Gleichungen: $x_3=5x_1-8$

    2. Einsetzen in E1: $x_2=4x_1-9$

    3. Aufstellen der Geradengleichung mit Ersetzen von $x_1$ durch den Parameter $r$:
    g: $\vec{x}=\left(\hspace{-1mm}\begin{array}{c} 0 \\ -9 \\ 8 \end{array}\hspace{-1mm}\right) + r\cdot \left(\hspace{-1mm}\begin{array}{c} 1 \\ 4 \\ 5 \end{array}\hspace{-1mm}\right)$

  1. 1. Aufstellen des LGS:
    \begin{array}{cccc} 2r &+s &-t &+u &=2 \\ &+s &+2t &-u &=4 \\ &-s &+4t &+3u &=2 \end{array}
    Das LGS ergibt die Lösung: $u=3-3t$.

    2. Einsetzen in Ebene E2:
    g: $\vec{x}=\left(\hspace{-1mm}\begin{array}{c} -2 \\ 5 \\ -8 \end{array}\hspace{-1mm}\right) + t\cdot \left(\hspace{-1mm}\begin{array}{c} 4 \\ -5 \\ 5 \end{array}\hspace{-1mm}\right)$


Wortliste und Satzbausteine



der Vektor, -en eine mathe­matische Größe mit einer Länge und Richtung
der Orts- oder Stützvektor, -en Der Ortsvektor zeigt vom Ursprung auf den Anfangs­punkt einer Geraden
der Richtungsvektor, -en gibt die Rich­tung von einem Punkt aus an
die Ebene, -n eine unendlich ausgedehnte Fläche im drei­dimensionalen Raum
die Parameter­form einer Ebene, -en wird durch einen Ortsvektor und zwei Richtungsvektoren mit Parameter beschrieben:
E: $\vec{x} = \vec{OA} + s\cdot\vec{u} + t\cdot\vec{v}$ mit $s, t \in \mathbb{R}$
die Koordinaten­form einer Ebene, -en $2x_1 - 5x_2 + 3x_3 = 4$ ist die Koordinaten­form einer Ebene
der Spur­punkt einer Ebene, -e Schnittpunkt der Ebene mit der Koordinatenachse
die Schnitt­gerade zweier Ebenen, -n Ebenen die nicht parallel sind schneiden sich entlang einer Geraden
© mylime.info