immer steiler werdende Bergwiese

Baumdiagramm - Mehrstufige Zufallsexperimente

Die Schweine lieben Bratwürstchen, jedoch nur aus Rindfleisch. Jetzt haben sich unter diese sechs Bratwürstchen zwei mit Schweinefleisch gemischt. Wie wahrscheinlich ist es, dass das erst Schwein eine Schweinsbratwurst isst? Mal angenommen, dass erste Schwein hatte Glück. Wie wahrscheinlich ist es dann, dass das zweite eine isst?

1 Kopf oder Zahl?
Euro-Münze

Einer der einfachsten Versuche ist der Münzwurf. Wirft man einmal, ist die Wahrscheinlichkeit für eine Zahl 50 %. Will man aber nochmal eine Zahl ist es nur noch 50 % von 50 % und das ist bekanntlich $0,5 \cdot 0,5=0,25$. Also beträgt die Wahrscheinlichkeit nur noch 25 %.

Um das ganze zu strukturieren hilft uns das Baumdiagramm.

2 Baumdiagramm - Pfadmultiplikations­regel
Baumdiagramm

Wie wahrscheinlich ist es 2mal Kopf zu werfen?

$$p_{2mal K}=\frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}$$

Pfadmultiplikationsregel:
Die Wahrscheinlichkeit eines Pfades ist gleich dem Produkt der Wahrscheinlichkeiten längs des Pfades.

3 Baumdiagram - Pfadadditions­regel
Baumdiagramm

Wie wahrscheinlich ist es 1mal Zahl zu werfen?

$$p_{1mal Z}=p_2+p_3=2 \cdot \frac{1}{4} = \frac{1}{2}$$

Pfadadditionsregel:
Gehören zu einem Ereignis mehrere Pfade, werden die Pfadwahrscheinlichkeiten addiert.

4 Limettenernte
Limettenbaum

Bei der jährlichen Limettenernte beträgt die Wahrscheinlichkeit eine faule Frucht zu erwischen 10 %. Die Wahrscheinlichkeit für eine gute Frucht beträgt somit $1-0,1=0,9$.

Wie hoch ist die Wahrscheinlichkeit bei dreimal Pflücken keine schlechte Frucht oder nur gute Früchte zu erhalten?

Auch hier hilft uns das Baumdiagramm.

5 Hochtourengehen
Hochtour

Beim Hochtourengehen gibt es etwa 0,5 % Unfälle.

Tom und Dan unternehmen jedes Jahr 2 Hochtouren. Wie wahrscheinlich ist es, dass sie keinen Unfall haben?

Wie wahrscheinlich ist das nach 7 Jahren?

Ein Baumdiagramm vereinfacht die Sache und gibt den Überblick

6 Qualität der Himbeeren
Himbeeren

Eine von 20 Himbeeren ist schlecht. Mario nimmt 5 Stück. Wie wahrscheinlich ist es dass er keine schlechte Himbeere nimmt?

Nutze das Baumdiagramm.

7 Schweinerei
Schweinerei

Die Schweine lieben Bratwürstchen, jedoch nur aus Rindfleisch. Jetzt haben sich unter fünf Bratwürstchen drei mit Schweinefleisch gemischt. Wie wahrscheinlich ist es, dass das erst Schwein eine Schweinsbratwurst isst?

Mal angenommen, dass erste Schwein hatte Glück. Wie wahrscheinlich ist es dann, dass das zweite eine isst?

Dieser Versuch unterscheidet sich von den Bisherigen: Die Würstchen werden nicht zurückgelegt. Es werden immer weniger und genau deshalb verändern sich die Wahrscheinlichkeiten.

8 Ziehen ohne Zurücklegen
Baumdiagramm

Merke: Bei mehrstufigen Zufallsexperimenten ohne Zurücklegen ändert sich die Gesamtzahl und damit die Wahrscheinlichkeit.

Die Wahrscheinlichkeit für 2mal Rindfleisch berechnet sich zu:

$$p_{RR}=\frac{2}{5} \cdot \frac{1}{4} = \frac{2}{20}= 10\:\%$$


Aufgabe 1 Würfeln

Renate würfelt mit fünf Würfeln. Zeichne das Baumdiagramm und bestimme die Wahrscheinlichkeit für

fünf Würfel

  1. fünfmal Eins.
  2. maximal zweimal eine Eins.
  1. $\left(\frac{1}{6}\right)^5$
  2. $1-\left(\frac{1}{6}\right)^5$

Entspann dich erst mal ...


Wahrscheinlichkeiten hin und her. Hier der wahrscheinlich coolste Dozent der Welt, oder sollte ich besser sagen: "der unwahrscheinlich schlechteste Dozent"?

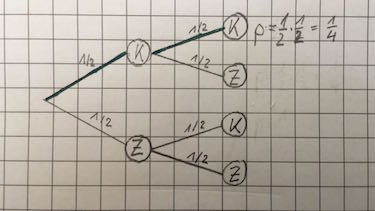
Aufgabe 2 Der Münzwurf

Gerd wirft siebenmal die Münze. Wie wahrscheinlich ist,

  1. keinmal Kopf,
  2. 7mal Kopf.
Euromünze

  1. $\left(\frac{1}{2}\right)^7$
  2. $\left(\frac{1}{2}\right)^7$


Aufgabe 3 Dreiecksroulette

Timo dreht das Dreieck dreimal. Bestimme mithilfe des Baumdiagramms die Wahrscheinlichkeit für

fünf Würfel

  1. zweimal drei.
  2. keinmal drei.
  3. mindestens zweimal drei.
  4. mindestens einmal drei.
  5. dreimal drei.
  1. Baumdiagramm:
    Baumdiagramm
    $p_{2mal\: 3}=\left(\frac{2}{27}\right)\cdot 3=\frac{6}{27}$
  1. $p_{0mal\: 3}=\left(\frac{2}{3}\right)^3=\frac{8}{27}$
  2. $p_{\geq 2mal\: 3}=\left(\frac{2}{27}\right)\cdot 3+\frac{1}{27}=\frac{7}{27}$
  3. $p_{\geq 1mal\: 3}=\left(\frac{27}{27}\right)- \frac{8}{27}=\frac{19}{27}$
  4. $p_{3mal\: 3}=\left(\frac{1}{3}\right)^3=\frac{1}{27}$

Aufgabe 4 Kugeln

Von acht Kugeln sind drei blau und fünf rot. Es wird dreimal ohne Zurücklegen gezogen.

  1. Zeichne das Baumdiagramm
  2. Wie wahrscheinlich zieht man zweimal rot?
  3. Wie wahrscheinlich zieht man zweimal blau?
Euromünze

  2. $3\cdot \frac{60}{336}=\frac{180}{336}$
  3. $3\cdot \frac{30}{336}=\frac{90}{336}$


Aufgabe 5 Mensch ägere dich nicht

Autoren: D. Welling, J. Blum, D. Supper | DFU und binnendifferenziert

Man würfelt 3mal, bei einer Sechs kommt man raus.

Spielfiguren

  1. Bestimme die Anzahl $n$ der Druchführungen, die Wahrscheinlichkeit $p$ bei einem Wurf eine 6 zu würfeln und die Gegenwahrscheinlichkeit $1-p$ bei einem Wurf keine 6 zu würfeln.

    Die Anzahl der Durchführungen entspricht hier der Wurfanzahl.

  2. Zeichne das mehrstufige Baumdiagramm. Beschrifte die Wahrscheinlichkeiten.

    Ein dreistufiges Baumdiagramm hat 8 Zweige. Startest Du von rechts nach links und beschriftest die Wahrscheinlichkeit oben, erhälst du eine saubere Struktur. Ergänze das abgebildete Baumdiagramm.

    Struktur eines dreistufigen Baumdiagramms

Bestimme bei 3 Würfen die Wahrscheinlichkeit,

  1. keinmal eine 6 zu würfeln,
  2. genau 2mal eine 6 zu würfeln,
  3. mindestens 2mal eine 6 zu würfeln,

    Addiere alle Wahrscheinlichkeiten der Pfade in denen mindestens 2mal die 6 vorkommt.

  4. 2mal hintereinader eine 6 zu würfeln,

    Du musst alle Pfade suchen, in denen 2mal hintereinander eine 6 gewürfelt wird. Addiere die Wahrscheinlichkeiten der Pfade.

    markierte Pfade mit mind. 2mal 6 hintereinander
  5. mindestens eine 6 zu würfeln.

    Da alle Pfadwahrscheinlichkeiten bis auf eine addiert werden müssen, kannst du auch von 100 % die Wahrscheinlichkeit des einen Pfades abziehen.

Im folgenden sollen die Anordnungsmöglichkeiten von Spielfiguren berechnet werden. Bestimme die Anordnungsmöglichkeiten für

  1. drei grüne und eine blaue Figur,
  2. eine rote, gelbe, grüne und blaue Figur.
  1. Anzahl der Durchführungen $n=3$,
    Wahrscheinlichkeit $p=1/6$,
    Gegenwahrscheinlichkeit $1-p=5/6$
  2. Baumdiagramm:
    Baumdiagramm
  1. $p_{\text{0mal 6}}=\frac{125}{216}$
  2. $p_{\text{2mal 6}}=\frac{15}{216}$
  3. $p_{\text{mindestens 2mal 6}}=\frac{16}{216}$
  4. $p_{\text{2mal hintereinander 6}}=\frac{11}{216}$
  5. $p_{\text{mindestens 1mal 6}}=\frac{91}{216}$
  6. Anordnungsmöglichkeiten: $4$
  7. Anordnungsmöglichkeiten: $4!=1\cdot 2 \cdot 3 \cdot 4 = 24$

Aufgabe 6 Die Socken

Autoren: D. Welling, J. Blum, D. Supper | DFU und binnendifferenziert

Beim Schulfest hat die Klasse 8a ein Gewinnspiel mit 3 Socken vorbereitet. Dazu soll vorher folgendes berechnet werden:

Socke 1: ❶ ❷ ❸ ❹ ❺ ❻ ❼

Socke 2: ❶ ❷ ❸ ❹ ❺ ❻

Socke 3: ❶ ❷ ❸ ❹


  1. Berechne wie hoch die Chance ist, jeweils aus einer Socke eine ❸ bei einmaligem Ziehen zu bekommen.
  2. Alex zieht dreimal mit Zurücklegen aus Socke 3. Berechne mit Hilfe eines Baumes die Wahrscheinlichkeit dafür, dass er dabei nur eine gerade Zahl zieht.
  3. Alexandra zieht zweimal ohne Zurücklegen aus Socke 3. Berechne mit Hilfe eines Baumes die Wahrscheinlichkeit dafür, dass sie dabei nur eine gerade Zahl zieht.
  4. Lina zieht 75mal aus Socke 1, dabei wird jede gezogene Kugel vor dem nächsten Zug zurückgelegt. Berechne wie oft sie in etwa in den 75 Versuchen die ❸ erwischt.

    Hier muss der Erwartungswert berechnet werden.

Tom zieht nacheinander aus allen drei Socken eine Kugel heraus. Berechne wie hoch die Chance ist

  1. 3mal eine ❸ zu ziehen,

    Zeichne ein Baumdiagramm. Die Wahrscheinlichkeiten ändern sich jedes mal, da jede Socke eine andere Anzahl an Kugeln hat.

  2. genau 1mal eine ❸ zu ziehen,
  3. keinmal eine ❸ zu ziehen.
  1. $p_{Socke 1}=\frac{1}{7}$, $p_{Socke 2}=\frac{1}{6}$, $p_{Socke 3}=\frac{1}{4}$
  2. $p=37,5\:\%$
  3. $p=2/3$
  4. $E\approx 11$
  5. Baumdiagramm:
    Baumdiagramm
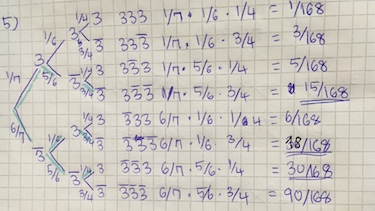
    $p_{3mal\:3}=\frac{1}{7} \cdot \frac{1}{6} \cdot \frac{1}{4}=\frac{1}{168}$
  6. $p_{1mal\:3}=\frac{15}{168} + \frac{18}{168} + \frac{30}{168}=\frac{63}{168}$
  7. $p_{0mal\:3}=\frac{6}{7} \cdot \frac{5}{6} \cdot \frac{3}{4}=\frac{90}{168}$


Aufgabe 7 Die Kisten mit den Bällen

Autoren: D. Welling, J. Blum, D. Supper | DFU und binnendifferenziert

Claus möchte – ohne zu gucken – einen blauen Ball aus einer der folgenden drei Kisten nehmen. Auf jeder Kiste steht, wie viele rote und blaue Bälle darin enthalten sind.

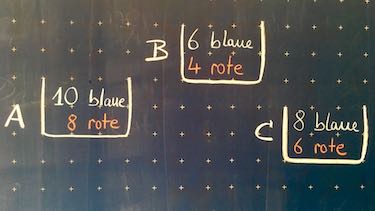
3 Kisten

  1. Ermittle die Kiste bei der die Wahrscheinlichkeit am größten ist, dass Claus einen blauen Ball herausnimmt.

Georg zieht dreimal aus Kiste B ohne Zurücklegen.

  1. Zeichne das mehrstufige Baumdiagramm. Beschrifte die Wahrscheinlichkeiten.

    Hinweis: Ein dreistufiges Baumdiagramm hat 8 Zweige. Startest Du von rechts nach links und beschriftest die Wahrscheinlichkeit oben, erhälst du eine saubere Struktur. Ergänze das abgebildete Baumdiagramm.

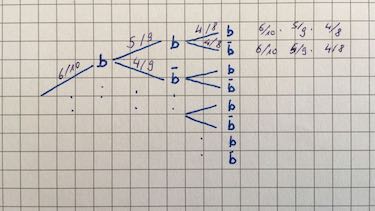
    Struktur eines dreistufigen Baumdiagramms

Bestimme bei 3maligen Ziehen aus Kiste B die Wahrscheinlichkeit,

  1. keinmal einen blauen Ball zu ziehen,
  2. genau 2mal einen blauen Ball zu ziehen,
  3. mindestens 2mal einen blauen Ball zu ziehen,

    Hinweis: Addiere alle Wahrscheinlichkeiten der Pfade in denen mindestens 2mal ein blauer Ball vorkommt.

  4. 2mal hintereinader einen blauen Ball zu ziehen,

    Hinweis: Du musst alle Pfade suchen, in denen 2mal hintereinander ein blauer Ball gezogen wird. Addiere die Wahrscheinlichkeiten der Pfade.

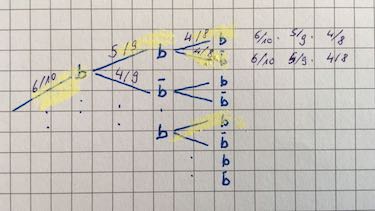
    markierte Pfade mit mind. 2mal blau hintereinander
  5. mindestens einen blauen Ball zu ziehen.

    Hinweis: Da alle Pfadwahrscheinlichkeiten bis auf eine addiert werden müssen, kannst du auch von 100 % die Wahrscheinlichkeit des einen Pfades abziehen.

  1. Wahrscheinlichkeiten:
    $p_{Kiste 1}=\frac{10}{18}\approx 0,56$
    $p_{Kiste 2}=\frac{6}{10}= 0,6$
    $p_{Kiste 3}=\frac{8}{14}\approx 0,57$
  2. Baumdiagramm:
    Baumdiagramm
  1. $p_{\text{0mal blau}}=\frac{1}{30}$
  2. $p_{\text{2mal blau}}=\frac{1}{2}$
  3. $p_{\text{mindestens 2mal blau}}=\frac{2}{3}$
  4. $p_{\text{2mal hintereinander blau}}=\frac{1}{2}$
  5. $p_{\text{mindestens 1mal blau}}=\frac{29}{30}$

Quiz 1 kahoot

Spiele gegen deine Mitschüler und gewinne.

  Los gehts   
kahoot

Aufgabe 8 Getränkeflaschen

Die Getränkeflaschen sollen angeordnet werden. Wie viele Anordnungsmöglichkeiten gibt es für

Flaschen

  1. eine Flasche?
  2. zwei Flaschen?
  3. drei Flaschen?
  4. vier Flaschen?
  5. fünf Flaschen?
  6. sechs Flaschen?
  7. n Flaschen?
  1. $1!$
  2. $2!$
  3. $3!$
  4. $4!$
  5. $5!$
  6. $6!$
  7. $n!$


Aufgabe 9 Farbfiguren

In einer Kiste befinden sich 7 gelbe, 5 blaue und 5 rote Figuren. Es wird 3mal ohne zurückzulegen gezogen. Zeichne ein vollständiges Baumdiagramm für die roten Figuren. Wie wahrscheinlich ist es

  1. 3mal eine rote Figur zu ziehen,
  2. genau 2mal eine rote Figur zu ziehen,
  3. genau einmal eine rote Figur zu ziehen,
  4. mindestens eine rote Figur zu ziehen,
  5. mindestens zwei rote Figuren zu ziehen?
Farbfiguren

  1. $p_{\text{3mal rot}}=\frac{5}{17}\cdot \frac{4}{16}\cdot \frac{3}{15}=\frac{60}{4080}$
  2. $p_{\text{2mal rot}}=3\cdot \frac{240}{4080}=\frac{720}{4080}$
  3. $p_{\text{1mal rot}}=3\cdot \frac{660}{4080}=\frac{1980}{4080}$
  4. $p_{\text{mind. 1mal rot}}=1- \frac{1320}{4080}=\frac{2760}{4080}$
  5. $p_{\text{mind. 2mal rot}}=\frac{720}{4080}+\frac{60}{4080}=\frac{780}{4080}$

Aufgabe 10 Neun Kugeln

Es wird 3mal ohne zurückzulegen gezogen. Wie wahrscheinlich ist es

❶ ❷ ❸ ❹

❺ ❻ ❼ ❽ ❾


  1. eine ❶ zu ziehen?
  2. eine ❶ ❷ ❸ zu ziehen?
  1. $p=\frac{1}{9} + \frac{8}{9} \cdot \frac{1}{8} + \frac{8}{9} \cdot \frac{7}{8} \cdot \frac{1}{7} = \frac{1}{3}$
  2. $p=\frac{1}{9}\cdot \frac{1}{8}\cdot\frac{1}{7}=\frac{1}{504}$



Wortliste und Satzbausteine



das Baum­diagramm, -e ein verzweigtes Schau­bild in der Wahrschein­lichkeitsrechnung
das Experi­ment, -e ein Versuch
die Wahr­schein­lich­keit, -en $p$ eine Einstufung von Aussagen auf deren Sicherheit
die Gegen­wahr­schein­lich­keit, -en $q=1-p$ die andere Wahrschein­lichkeit bei einem Ex­periment mit 2 Ergebnissen
die An­zahl der Ex­peri­mente $n$ die Menge der hinter­einander durch­geführten Versuche
die Pfad­multipli­kations­regel, -n Die Wahrschein­lichkeit eines Pfades ist gleich dem Produkt der Wahrschein­lichkeiten längs des Pfades.
die Pfad­additions­regel, -n Gehören zu einem Ereignis mehrere Pfade, werden die Pfad­wahrschein­lich­keiten addiert.

© mylime.info