mylime - Mathe

1 Flächen anmalen

Um die notwendige Farbmenge abzuschätzen, benötigen wir den entsprechenden Flächeninhalt.

Manchmal bestehen die Flächen dabei aus einfachen geometrischen Formen. Häufig jedoch setzen sich die Flächen aus unterschiedlichen Figuren zusammen. Die Fläche eines Fingernagels könnte man bspw. aus einem Quadrat mit zwei Halbkreisen nähern.

Ist man in der Lage von bestimmten Figuren die Flächen zu berechnen, lässt sich so einfach eine zusammengesetzte Fläche berechnen.

2 Das Rechteck

Stelle alle Stühle im Klassenraum zu einer möglichst großen rechteckigen Fläche zusammen. Ermittle die Anzahl der Stühle indem du möglichst wenig Stühle zählst.

Man erhält bspw. einen Flächeninhalt $A=4\cdot 8=24$. Flächeninhalte von Rechtecken und Quadraten berechnet man zu:

$$A = a \cdot b$$

Beantworte folgende Fragen: Wie ändert sich die Fläche, wenn das Rechteck um eine Reihe erweitert wird? Wie viele Reihen muss man dazu stellen damit sich die Fläche verdoppelt? Worauf musst du beim Zählen der Reihen und Spalten achten?

3 Das Dreieck

Ein Dreieck lässt sich zu einem Rechteck erweitern. Dabei hat das Rechteck die doppelte Fläche, wie das Dreieck. Somit können wir schreiben:

$$A_\Delta = \frac{a \cdot h_a}{2}$$

Dabei ist $a$ die Länge der Grundseite und $h_a$ die zugehörige Höhe.

4 Das Parallelogramm

Das Parallelogramm lässt sich relativ einfach zu einem Rechteck zerlegen, indem man ein Dreieck auf einer Seite abschneidet und auf der gegenüberliegen Seite ansetzt. So erhält man die Fläche über die Länge der Grundseite $a$ und der zugehörigen Höhe $h$:

$$A=a \cdot h$$

5 Der Kreis

Nimm einen Muffin oder einen Keks und zeichne einen entsprechenden Kreis in dein Heft. Wie kannst du den Umfang und den Durchmesser des Kreises bestimmen?

Welche Zahl erhälst du, wenn du den Umfang durch den Durchmesser teilst?

Die Kreiszahl $\pi$ (Pi) ist das Verhältnis von Umfang $u$ zu Durchmesser $d$:

$$\pi=u/d=3.1415926...$$

Ein Kreis mit einem Radius von 1 m hat somit einen Umfang von $2\pi$. Diese Kreiszahl $\pi$ findet man schon bei den Ägyptern und in der Bibel.

6 Kreisfläche

Die Zahl $\pi$ ist nicht periodisch, d.h. es gibt kein sich wiederholendes Muster. Dies ist in dem Video sehr schön dargestellt.

Teilt man einen Kreis in ganz viele Stücke erhält man näherungsweise viele kleine Dreiecke, von denen man die Fläche und somit die Kreisfläche bestimmen kann:

$$A=\pi \cdot r^2$$

Tipp: Solltest du nicht mit dem Taschenrechner arbeiten empfiehlt es sich, die Zahl $\pi$ auf zwei Nachkommastellen zu begrenzen.

7 Trapez und zusammengesetzte Figuren

Viele Figuren im Alltag sind aus anderen zusammengesetzt und können mit Hilfe von einfachen Figuren berechnet werden.

Die Honigwabe könnte man bspw. jeweils aus zwei Trapezen zusammensetzen. Mit Hilfe des Rechtecks kann dann der Flächeninhalt des Trapezes berechnet werden:

$$A=(a-\frac{a-c}{2}) \cdot h$$

Ideen: P. Wunderlich, Seminar Weingarten
H. Griesel et al., "Elemente der Mathematik", Band 1+2, Schroedel Verlag, 2004

Aufgabe 1 Anzahl an Farbdosen und Karokästchen

Eine Farbpalette hat in einer Reihe 12 und in einer Spalte 7 Dosen. Berechne die Anzahl der Dosen.

Berechne die Anzahl von Karokästchen auf einem DIN A4 Blatt.

Berechne die Fläche eines Schultisches.
Wie groß ist die Fläche aller Schultische in einem Klassenzimmer?

Berechne die Fläche eines Kästchens wenn der Zauberwürfel eine Kantenlänge von 4 cm hat.

Die Farbpalette hat $12\cdot 7 = 84$ Dosen.

Ein DIN A4 Blatt hat 2748 Kästchen, wenn man die halben Kästchen am Rand addiert.

Ein Schultisch hat beispielweise eine Fläche von: $A=50\cdot 130=6.500\:\text{cm}^2$. Bei 12 Tischen im Raum macht dies eine Gesamtfläche von $A=12\cdot 6.500=78.000\:\text{cm}^2$

Der Zauberwürfel:
Eine Seite hat $3\cdot 3 = 9$ Kästchen.
Insgesamt hat der Würfel $6 \cdot 9=54$ Kästchen.
Die Seitenfläche eines Würfels beträgt: $4\cdot 4=16$ cm² und ein Kästchen hat eine Fläche von $16:9=16/9$ cm².
Die Gesamtfläche des Würfels beträgt $16/9\cdot 54=96$ cm².

Aufgabe 2 Dreieck

Zeichne die folgenden Dreiecke in ein Koordinatensysteme und berechne die Fläche:

A(1|1), B(7|1), C(7|5)
A(1|1), B(7|1), C(5|4)
A(1|1), B(7|1), C(9|4)

A(1|1), B(7|1), C(7|5): $A=6 \cdot 4 /2 = 12$
A(1|1), B(7|1), C(5|4): $A=6 \cdot 3 /2 = 9$
A(1|1), B(7|1), C(9|4): $A=6 \cdot 3 /2 = 9$

Aufgabe 3 Turm in Stadtmauer

Glurns im Vinschgau (Südtirol - Italien) ist eine der kleinsten Alpenstädte. Die Besonderheit: Die Stadtmauern von Glurns sind vollständig erhalten.

Berechne die Querschnittsfläche des Turms. Er hat einen Durchmesser von 2,50 und eine Höhe (ohne Dach) von 4 m. Das Dach ist 2 m hoch.

Lösungsvorschlag: $A=2,5 \cdot 4 + 2,5 \cdot 2 / 2$

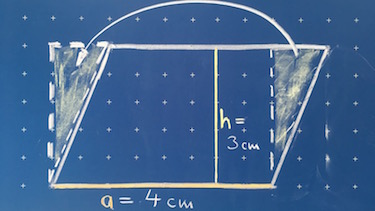
Aufgabe 4 Paralellogramme im Vergleich

Übertrage die drei Parallelogramme in dein Heft und berechne deren Fläche.

Welcher Einfluß hat die Schräge auf den Flächeninhalt?

Wie viel Farbe zum anmalen benötigst du, wenn du das Parallelogramm unendlich schräg machst?

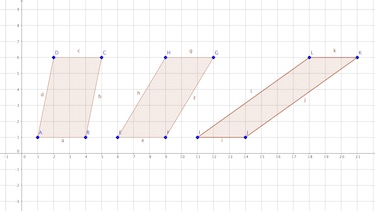
Fläche: $A=3\cdot 5 = 15$

Aufgabe 5 Flächeninhalt Parallelogramm

Zeichne das Parallelogramm ABCD in ein Koordinatensystem. Berechne dann ohne zu messen den Flächeninhalt.

A(0|1), B(7|1), C(10|4), D(3|4)
A(0|2), B(8|2), C(10|4), D(2|4)
A(-1|-2), B(4|-2), C(5|1), D(0|1)
Berechne die Fläche des ersten Parallelogramms mithilfe 2er Dreiecke und eines Rechtecks.

A(0|1), B(7|1), C(10|4), D(3|4): $A=7\cdot 3$
A(0|2), B(8|2), C(10|4), D(2|4): $A=8\cdot 2$
A(-1|-2), B(4|-2), C(5|1), D(0|1): $A=5\cdot 3$

Aufgabe 6 Fehlende Größen

Berechne die fehlende Größe des Parallelogramms.

Seitenlänge a	zugehörige Höhe h	Flächeninhalt A
12	4
2		8
	4	9
2.5	4.2
	4	13.3

Seitenlänge a	zugehörige Höhe h	Flächeninhalt A
12	4
2		8
	4	9
2.5	4.2
	4	13.3

Aufgabe 7 Kreisflächen

Der Mühlstein hat einen Durchmesser von 1,60 m. Der innere Kreis hat einen Durchmesser von 0,2 m.

Berechne die Fläche des äußeren Kreises.
Berechne die Fläche des inneren Kreises.
Berechne die Steinfläche.

Fläche des äußeren Kreises: $A=2,0096$ m²
Fläche des inneren Kreises: $A=0,0314$ m²
Steinfläche: $A=1,9782$ m²

Aufgabe 8 Pizza

In einer Pizzeria werden die Größe S mit einem Durchmesser von 22 cm für 5,60 EUR und die Größe L mit einem Durchmesser von 30 cm für 8,30 EUR angeboten.

Bei welcher Pizzagröße bekommt man mehr für sein Geld?

Lösungshinweis:
1. Flächeninhalte berechnen.
2. Preis pro cm² berechnen.

Aufgabe 9 Trapez

Berechne den Flächeninhalt ...

eines Trapezes mit a = 8 cm, c = 4 cm und h = 3 cm.
eines Trapezes mit a = 4 cm, c = 2 cm und h = 2 cm.
einer Honigwabe, wenn der längste Abstand 1,5 cm und der kürzeste Abstand 1 cm lang ist.

A = 18 cm²
A = 6 cm²
A = 1 cm²

Aufgabe 10 Zusammengesetzte Figuren

Berechne den Flächeninhalt und Umfang

Figur 1 - Hinweis: Die Schräge hat eine Länge von 1,41 cm

Figur 2 - Hinweis: Die Schrägen haben eine Länge von 0,71 cm und 1,12 cm.

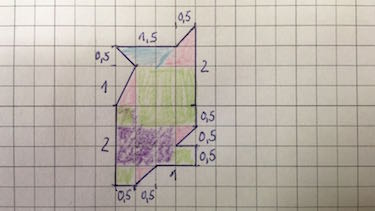
A = 13,07 cm²
u = 16,55 cm
A = 6,00 cm²
u = 12,46 cm

Wortliste und Satzbausteine

der Flächeninhalt, -e	Maß für die Größe einer Fläche
das Rechteck, -e	eine geometrische Figur mit vier rechten Winkeln (90 °)
das Quadrat, -e	ein Rechteck mit vier gleich langen Seiten
der Flächeninhalt eines Dreiecks, -e	Der Flächeninhalt eines Dreiecks berechnet sich mit der Grundseite $a$ und der zugehörigen Höhe $h_a$ zu: $A_{\Delta}=\frac{a\cdot h_a}{2}$
das Parallelogramm, -e	ein Viereck mit jeweils zwei parallelen Seiten
der Flächeninhalt eines Parallelogramms, -e	Der Flächeninhalt eines Parallelogramms berechnet sich mit der Grundseite $a$ und der zugehörigen Höhe $h$ zu: $A=a\cdot h$

der Umfang $u$ eines Kreises, -"e	die Strecke der gesamten Kreislinie
die Kreiszahl $\pi$ (Pi), -en	Die Kreiszahl $\pi$ ist das Verhältnis aus Umfang $u$ und Durchmesser $d$ eines Kreises: $\pi=\frac{u}{d}=3,1415926...$
der Flächeninhalt eines Kreises, -e	Der Flächeninhalt eines Kreises ist das Produkt aus Kreiszahl und dem Radius im Quadrat: $A=\pi \cdot r^2$
die Palette, -n	eine rechteckige Konstruktion, die den Transport einer Vielzahl an Waren ermöglicht
die Reihe, -n	die waagerechte Anordnung von Gegenständen oder Werten
die Spalte, -n	die senkrechte Anordnung von Gegenständen oder Werten.

Flächeninhalte von Figuren